6.1 Integrability properties of Killing fields
Our aim here is to discuss the circularity problem in some more detail. We refer the reader to
Section 2.1 and Section 3.5 for the general context and for references concerning the staticity and the
circularity issues. In both cases, the task is to use the symmetry properties of the matter model in order to
establish the Frobenius integrability conditions for the Killing field(s). The link between the relevant
components of the stress-energy tensor and the integrability conditions is provided by a general identity for
the derivative of the twist of a Killing field 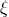 , say,
and Einstein’s equations, implying
, say,
and Einstein’s equations, implying
![ξ ∧ R (ξ ) = 8 π[ξ ∧ T (ξ)]](article469x.gif) .
For a stationary and axisymmetric spacetime with Killing fields (one-forms)
.
For a stationary and axisymmetric spacetime with Killing fields (one-forms) 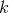 and
and 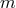 , Eq. (49)
implies
and similarly for
, Eq. (49)
implies
and similarly for 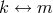 .
By virtue of Eq. (50) – and the fact that the Frobenius condition
.
By virtue of Eq. (50) – and the fact that the Frobenius condition 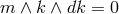 can be written as
can be written as
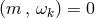 – the circularity problem is reduced to the following two tasks:
– the circularity problem is reduced to the following two tasks:
(i) Show that 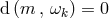 implies
implies 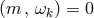 .
.
(ii) Establish 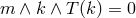 from the stationary and axisymmetric matter equations.
from the stationary and axisymmetric matter equations.
(i) Since 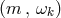 is a function, it must be constant if its derivative vanishes. As
is a function, it must be constant if its derivative vanishes. As 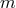 vanishes on the
rotation axis, this implies
vanishes on the
rotation axis, this implies 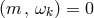 in every domain of spacetime intersecting the axis. (At this point
it is worthwhile to recall that the corresponding step in the staticity theorem requires more effort:
Concluding from
in every domain of spacetime intersecting the axis. (At this point
it is worthwhile to recall that the corresponding step in the staticity theorem requires more effort:
Concluding from 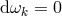 that
that 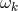 vanishes is more involved, since
vanishes is more involved, since 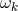 is a one-form. However, using
Stoke’s theorem to integrate an identity for the twist [88
is a one-form. However, using
Stoke’s theorem to integrate an identity for the twist [88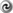 ] shows that a strictly stationary –
not necessarily simply connected – domain of outer communication must be static if
] shows that a strictly stationary –
not necessarily simply connected – domain of outer communication must be static if 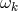 is
closed.)
is
closed.)
(ii) While 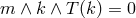 follows from the symmetry conditions for electro-magnetic fields [27] and
for scalar fields [86], it cannot be established for non-Abelian gauge fields [88]. This implies that the usual
foliation of spacetime used to integrate the stationary and axisymmetric Maxwell equations
is too restrictive to treat the Einstein–Yang–Mills (EYM) system. This is seen as follows: In
Section (4.4) we have derived the formula (22). By virtue of Eq. (10) this becomes an expression for
the derivative of the twist in terms of the electric Yang–Mills potential
follows from the symmetry conditions for electro-magnetic fields [27] and
for scalar fields [86], it cannot be established for non-Abelian gauge fields [88]. This implies that the usual
foliation of spacetime used to integrate the stationary and axisymmetric Maxwell equations
is too restrictive to treat the Einstein–Yang–Mills (EYM) system. This is seen as follows: In
Section (4.4) we have derived the formula (22). By virtue of Eq. (10) this becomes an expression for
the derivative of the twist in terms of the electric Yang–Mills potential 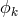 (defined with
respect to the stationary Killing field
(defined with
respect to the stationary Killing field 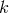 ) and the magnetic one-form
) and the magnetic one-form 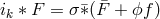 :
:
Contracting this relation with the axial Killing field 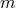 , and using again the fact that the Lie derivative of
, and using again the fact that the Lie derivative of
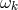 with respect to
with respect to 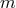 vanishes, yields immediately
The difference between the Abelian and the non-Abelian case lies in the circumstance
that the Maxwell equations automatically imply that the
vanishes, yields immediately
The difference between the Abelian and the non-Abelian case lies in the circumstance
that the Maxwell equations automatically imply that the 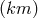 -component of
-component of 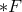 vanishes,
whereas this does not follow from the Yang–Mills equations. Moreover, the latter do not imply that the Lie
algebra valued scalars
vanishes,
whereas this does not follow from the Yang–Mills equations. Moreover, the latter do not imply that the Lie
algebra valued scalars 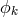 and
and 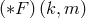 are orthogonal. Hence, circularity is a generic property of the
Einstein–Maxwell (EM) system, whereas it imposes additional requirements on non-Abelian gauge
fields.
are orthogonal. Hence, circularity is a generic property of the
Einstein–Maxwell (EM) system, whereas it imposes additional requirements on non-Abelian gauge
fields.
Both the staticity and the circularity theorems can be established for scalar fields or, more generally,
scalar mappings with arbitrary target manifolds: Consider a self-gravitating scalar mapping
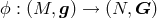 with Lagrangian
with Lagrangian ![L[ϕ,d ϕ,g,G ]](article512x.gif) . The stress energy tensor is of the form
. The stress energy tensor is of the form
where the functions 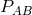 and
and 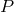 may depend on
may depend on  ,
, 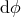 , the spacetime metric
, the spacetime metric 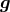 and the target
metric
and the target
metric 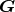 . If
. If 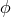 is invariant under the action of a Killing field
is invariant under the action of a Killing field 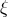 – in the sense that
– in the sense that 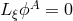 for
each component
for
each component 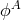 of
of 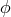 – then the one-form
– then the one-form 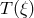 becomes proportional to
becomes proportional to 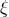 :
: 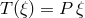 . By
virtue of the Killing field identity (49), this implies that the twist of
. By
virtue of the Killing field identity (49), this implies that the twist of 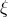 is closed. Hence, the staticity and
the circularity issue for self-gravitating scalar mappings reduce to the corresponding vacuum problems.
From this one concludes that stationary non-rotating black hole configuration of self-gravitating
scalar fields are static if
is closed. Hence, the staticity and
the circularity issue for self-gravitating scalar mappings reduce to the corresponding vacuum problems.
From this one concludes that stationary non-rotating black hole configuration of self-gravitating
scalar fields are static if 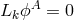 , while stationary and axisymmetric ones are circular if
, while stationary and axisymmetric ones are circular if
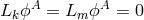 .
.
![]() implies
implies ![]() .
.
![]() from the stationary and axisymmetric matter equations.
from the stationary and axisymmetric matter equations.
![]() is a function, it must be constant if its derivative vanishes. As
is a function, it must be constant if its derivative vanishes. As ![]() vanishes on the
rotation axis, this implies
vanishes on the
rotation axis, this implies ![]() in every domain of spacetime intersecting the axis. (At this point
it is worthwhile to recall that the corresponding step in the staticity theorem requires more effort:
Concluding from
in every domain of spacetime intersecting the axis. (At this point
it is worthwhile to recall that the corresponding step in the staticity theorem requires more effort:
Concluding from ![]() that
that ![]() vanishes is more involved, since
vanishes is more involved, since ![]() is a one-form. However, using
Stoke’s theorem to integrate an identity for the twist [88
is a one-form. However, using
Stoke’s theorem to integrate an identity for the twist [88![]() ] shows that a strictly stationary –
not necessarily simply connected – domain of outer communication must be static if
] shows that a strictly stationary –
not necessarily simply connected – domain of outer communication must be static if ![]() is
closed.60)
is
closed.60)
![]() follows from the symmetry conditions for electro-magnetic fields [27] and
for scalar fields [86], it cannot be established for non-Abelian gauge fields [88]. This implies that the usual
foliation of spacetime used to integrate the stationary and axisymmetric Maxwell equations
is too restrictive to treat the Einstein–Yang–Mills (EYM) system. This is seen as follows: In
Section (4.4) we have derived the formula (22
follows from the symmetry conditions for electro-magnetic fields [27] and
for scalar fields [86], it cannot be established for non-Abelian gauge fields [88]. This implies that the usual
foliation of spacetime used to integrate the stationary and axisymmetric Maxwell equations
is too restrictive to treat the Einstein–Yang–Mills (EYM) system. This is seen as follows: In
Section (4.4) we have derived the formula (22![]() ). By virtue of Eq. (10
). By virtue of Eq. (10![]() ) this becomes an expression for
the derivative of the twist in terms of the electric Yang–Mills potential
) this becomes an expression for
the derivative of the twist in terms of the electric Yang–Mills potential ![]() (defined with
respect to the stationary Killing field
(defined with
respect to the stationary Killing field ![]() ) and the magnetic one-form
) and the magnetic one-form ![]() :
:
![]() with Lagrangian
with Lagrangian ![]() . The stress energy tensor is of the form
. The stress energy tensor is of the form