5.3 The Israel–Wilson class
A particular class of solutions to the stationary EM equations is obtained by requiring
that the Riemannian manifold 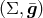 is flat [102
is flat [102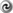 ]. For
]. For 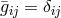 , the three-dimensional
Einstein equations obtained from variations of the effective action (28) with respect to
, the three-dimensional
Einstein equations obtained from variations of the effective action (28) with respect to 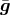 become
Israel and Wilson [102
become
Israel and Wilson [102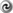 ] have shown that all solutions of this equation fulfill
] have shown that all solutions of this equation fulfill 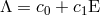 . In fact, it is not
hard to verify that this ansatz solves Eq. (43), provided that the complex constants
. In fact, it is not
hard to verify that this ansatz solves Eq. (43), provided that the complex constants 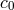 and
and 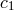 are
subject to
are
subject to 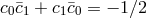 . Using asymptotic flatness, and adopting a gauge where the
electro-magnetic potentials and the twist potential vanish in the asymptotic regime, one has
. Using asymptotic flatness, and adopting a gauge where the
electro-magnetic potentials and the twist potential vanish in the asymptotic regime, one has 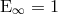 and
and
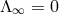 , and thus
It is crucial that this ansatz solves both the equation for
, and thus
It is crucial that this ansatz solves both the equation for 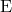 and the one for
and the one for 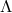 : One easily verifies that
Eqs. (29) reduce to the single equation
where
: One easily verifies that
Eqs. (29) reduce to the single equation
where 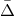 is the three-dimensional flat Laplacian.
is the three-dimensional flat Laplacian.
For static, purely electric configurations the twist potential 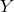 and the magnetic potential
and the magnetic potential 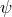 vanish.
The ansatz (44), together with the definitions of the Ernst potentials,
vanish.
The ansatz (44), together with the definitions of the Ernst potentials, 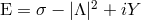 and
and
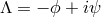 (see Section 4.5), yields
(see Section 4.5), yields
Since 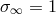 , the linear relation between
, the linear relation between 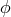 and the gravitational potential
and the gravitational potential 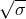 implies
implies
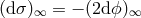 . By virtue of this, the total mass and the total charge of every asymptotically flat,
static, purely electric Israel–Wilson solution are equal:
where the integral extends over an asymptotic
two-sphere.
The simplest nontrivial solution of the flat Poisson equation (45),
. By virtue of this, the total mass and the total charge of every asymptotically flat,
static, purely electric Israel–Wilson solution are equal:
where the integral extends over an asymptotic
two-sphere.
The simplest nontrivial solution of the flat Poisson equation (45), 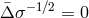 , corresponds to a linear
combination of
, corresponds to a linear
combination of 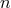 monopole sources
monopole sources 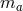 located at arbitrary points
located at arbitrary points 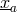 ,
This is the Papapetrou–Majumdar (PM) solution [143, 128], with spacetime metric
,
This is the Papapetrou–Majumdar (PM) solution [143, 128], with spacetime metric
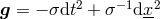 and electric potential
and electric potential 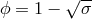 . The PM metric describes
a regular black hole spacetime, where the horizon comprises
. The PM metric describes
a regular black hole spacetime, where the horizon comprises 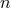 disconnected
components.
In Newtonian terms, the configuration corresponds to
disconnected
components.
In Newtonian terms, the configuration corresponds to 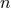 arbitrarily located charged mass points with
arbitrarily located charged mass points with
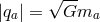 . The PM solution escapes the uniqueness theorem for the Reissner–Nordström metric,
since the latter applies exclusively to space-times with
. The PM solution escapes the uniqueness theorem for the Reissner–Nordström metric,
since the latter applies exclusively to space-times with 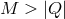 .
.
Non-static members of the Israel–Wilson class were constructed as well [102, 145]. However, these
generalizations of the Papapetrou–Majumdar multi black hole solutions share certain unpleasant properties
with NUT spacetime [140] (see also [16, 136]). In fact, the work of Hartle and Hawking [81], and
Chruściel and Nadirashvili [42] strongly suggests that – except the PM solutions – all configurations
obtained by the Israel–Wilson technique are either not asymptotically Euclidean or have naked singularities.
In order to complete the uniqueness theorem for the PM metric among the static black hole solutions with
degenerate horizon, it basically remains to establish the equality 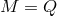 under the assumption that the
horizon has some degenerate components. Until now, this has been achieved only by requiring that all
components of the horizon have vanishing surface gravity and that all “horizon charges” have the same
sign [90].
under the assumption that the
horizon has some degenerate components. Until now, this has been achieved only by requiring that all
components of the horizon have vanishing surface gravity and that all “horizon charges” have the same
sign [90].
![]() and the magnetic potential
and the magnetic potential ![]() vanish.
The ansatz (44
vanish.
The ansatz (44![]() ), together with the definitions of the Ernst potentials,
), together with the definitions of the Ernst potentials, ![]() and
and
![]() (see Section 4.5), yields
(see Section 4.5), yields ![]() under the assumption that the
horizon has some degenerate components. Until now, this has been achieved only by requiring that all
components of the horizon have vanishing surface gravity and that all “horizon charges” have the same
sign [90].
under the assumption that the
horizon has some degenerate components. Until now, this has been achieved only by requiring that all
components of the horizon have vanishing surface gravity and that all “horizon charges” have the same
sign [90].