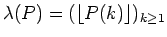
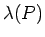
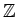
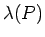
We study the uniform distribution of the polynomial sequence modulo integers, where P(x) is a polynomial with real coefficients. In the nonlinear case, we show that is uniformly distributed in if and only if P(x) has at least one irrational coefficient other than the constant term. In the case of even degree, we prove a stronger result: intersects every congruence class modulo every integer if and only if P(x) has at least one irrational coefficient other than the constant term.