Let
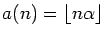
and
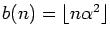
,
where
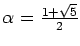
.
Then a theorem of Carlitz et al. states that each
function
f, composed of several
a's and
b's, can be expressed in
the form
c1a +
c2b -
c3, where
c1 and
c2 are consecutive
Fibonacci numbers determined by the numbers of
a's and of
b's
composing
f and
c3 is a nonnegative constant. We provide
generalizations of this theorem to two infinite families of
complementary pairs of Beatty sequences. The particular case involving
`Narayana' numbers is examined in depth. The details reveal that
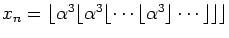
,
with
n nested
pairs of

,
is a 7th-order linear recurrence, where
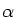
is the
dominant zero of
x3 -
x2 - 1.
Received July 26 2016; revised versions received January 17 2017; January 28 2017.
Published in Journal of Integer Sequences, January 28 2017. Minor
revision, July 30 2017.

