| |
|
|
| |
Volume 7, Issue 2, Article 65 |
|
|
|
|
|
| |
On an Inequality Involving Power and Contraction of Matrices with and without Trace
|
| |
|
Authors: |
Marcos V. Travaglia, |
|
| |
|
Keywords:
|
Trace inequalities, Operator inequalities, Positive semidefinite matrix, Operator monotony, Operator concavity. |
|
| |
|
Date Received:
|
28/01/06 |
|
| |
|
Date Accepted:
|
16/02/06 |
|
| |
|
Subject Codes: |
15A45, 15A90, 47A63.
|
|
| |
|
Editors: |
Frank Hansen, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
Let 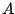 and and 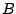 be positive semidefinite matrices. Assuming that the eigenvalues of be positive semidefinite matrices. Assuming that the eigenvalues of 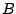 are less than one, we prove the following trace inequalities are less than one, we prove the following trace inequalities
and
for all 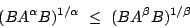
in the cases (a)  or (b) or (b) 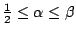 and and 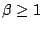 . Further we present counterexamples involving . Further we present counterexamples involving 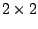 matrices showing that the last inequality is, in general, violated in case that neither (a) nor (b) is fulfilled. matrices showing that the last inequality is, in general, violated in case that neither (a) nor (b) is fulfilled.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|



