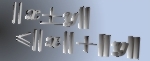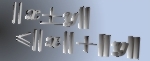| |
|
|
| |
Volume 6, Issue 2, Article 29 |
|
|
|
|
|
| |
Equations and Inequalities Involving $v_p(n!)$
|
| |
|
Authors: |
Mehdi Hassani, |
|
| |
|
Keywords:
|
Factorial function, Prime number, Inequality. |
|
| |
|
Date Received:
|
14/06/04 |
|
| |
|
Date Accepted:
|
16/02/05 |
|
| |
|
Subject Codes: |
05A10, 11A41, 26D15, 26D20.
|
|
| |
|
Editors: |
László Tóth, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
In this paper we study 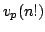 , the greatest power of prime , the greatest power of prime 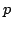 in factorization of in factorization of 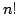 . We find some lower and upper bounds for . We find some lower and upper bounds for 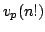 , and we show that , and we show that 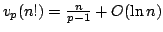 . By using the afore mentioned bounds, we study the equation . By using the afore mentioned bounds, we study the equation 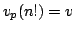 for a fixed positive integer for a fixed positive integer 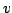 . Also, we study the triangle inequality about . Also, we study the triangle inequality about 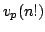 , and show that the inequality , and show that the inequality 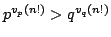 holds for primes holds for primes 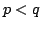 and sufficiently large values of and sufficiently large values of 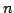 . .
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|