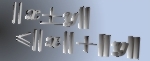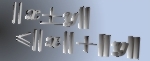| |
|
|
| |
Volume 10, Issue 3, Article 62 |
|
|
|
|
|
| |
A Matrix Inequality for Möbius Functions
|
| |
|
Authors: |
Olivier Bordellčs, Benoit Cloitre, |
|
| |
|
Keywords:
|
Determinants, Dirichlet convolution, Möbius functions, Singular values. |
|
| |
|
Date Received:
|
24/11/2008 |
|
| |
|
Date Accepted:
|
27/03/2009 |
|
| |
|
Subject Codes: |
15A15, 11A25, 15A18, 11C20.
|
|
| |
|
Editors: |
László Tóth, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
The aim of this note is the study of an integer matrix whose determinant is related to the Möbius function. We derive a number-theoretic inequality involving sums of a certain class of Möbius functions and obtain a sufficient condition for the Riemann hypothesis depending on an integer triangular matrix. We also provide an alternative proof of Redheffer's theorem based upon a LU decomposition of the Redheffer's matrix.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|