evolvent of a circle
by a simple mechanical procedure), a logarithmic
spiral is often replaced by an equidistant spiral. That results
in a disturbance of the equiangularity and equiformity, and
consequently, of the similarity symmetry.
The basic visual-symbolic characteristic of the symmetry
group L is a double visual dynamism, caused by the visual
suggestion of a rotational motion and centrifugal expansion,
resulting from the rotational and dilatational component. Polar
radial rays exist under the condition that q = pp/q,
(p,q) = 1, p,q Î Z. A degree of the visual dynamism produced
by corresponding similarity symmetry rosettes depends on the
coefficient k and on the dilative rotation angle q.
Changes in these parameters result in different visual
impressions.
The symmetry group L is applied in painting works having the
central perspective as the element, or even as a basis of the complete
central dynamic composition of the work (e.g., in the baroque, in
Tintoretto's works), creating thus the visual impression of an expanding
rotational motion.
Similarity symmetry groups the type CnL (nL) are
formed by composing the symmetry groups L and Cn (n) with
the same invariant point. Corresponding similarity symmetry groups can be
constructed multiplying by the dilative rotation L a figure with the
symmetry group Cn (n), belonging to a fundamental region of the
symmetry group L, or multiplying by the n-fold rotation a figure
with the symmetry group L, belonging to a fundamental region of the
symmetry group Cn (n) (Figure 3.9a, 3.10). In both cases the
rotation center and dilative rotation center coincide. Constructional
methods used are analogous to that considered with the symmetry
group L. In ornamental art, especially when the metric
construction method is applied, deviations from the regularity
dictated by the metric property of the dilative rotation L,
frequently occur. A tendency toward maximal constructional
simplicity results in the appearance of the equidistance,
disturbance of the equiangularity and equiformity,
desymmetrization of the similarity symmetry group CnL
(nL) and its reduction to the symmetry group Cn
(n).
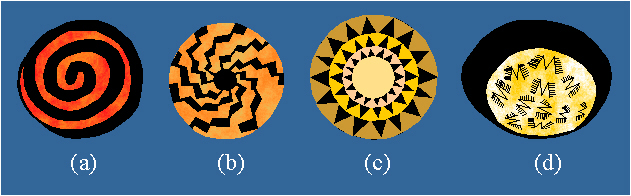
Figure 3.9
|
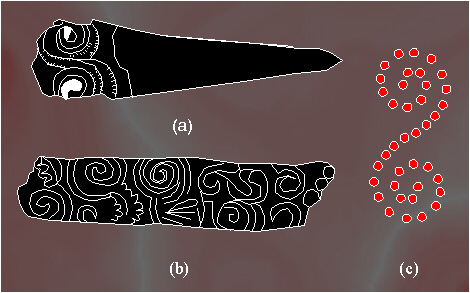
Examples of similarity symmetry rosettes in the art of Neolithic and
pre-dynastic period of the ancient civilizations, around 4500-3500
B.C.: (a) Egypt; (b), (c) examples of rosettes with the similarity
symmetry group of the type CnL (nL) and DnL (nmL),
Egypt and Iran; (d) example of the rosette with the similarity
symmetry group of the type DnL (nmL), Susa ceramics.
|

Figure 3.10
|
Examples of ornamental motifs in the ceramics of the American Indians,
that suggest similarity symmetry.
|
By applying the criterion of maximal symmetry, it is possible to
eliminate certain repetitions and overlappings of symmetry groups, otherwise
occurring within the type CnL (nL). The existence of the
n-fold rotation with the rotation angle 2p/n and the dilative
rotation L with the dilative rotation angle q (for k > 0) or (
p-q) (for k < 0), within the symmetry group CnL (nL)
results in the appearance of the new dilative rotation L' with the minimal
dilative rotation angle q', which is less than the dilative
rotation angle q. According to the criterion of maximal symmetry,
every symmetry group CnL (nL) can be considered as the symmetry
group CnL' (nL'). If we accept the condition
CnL0=CnL(k,0) = CnK, the type CnK
(nK) is the subtype of the type CnL (nL).
For n - an odd natural number and k < 0 , the relationship
CnL2n=CnL(k,p/n) = CnK
(|k|) = CnK holds. For n - an odd natural
number, according to the above relationship and the relationship
CnK=CnL2n, holding for n - an odd
natural number and k < 0, we can conclude that the types
CnK (nK) and CnL2n (nL2n), are
dual with respect to the change of the sign of the coefficient
k.
A fundamental region of the symmetry group CnL (nL) is
the section of the fundamental regions of its generating symmetry groups
Cn (n) and L with the same invariant point. Between
symmetry groups of the type CnL (nL) there will be no essential
difference depending on the sign of the coefficient k. Since examples of
rosettes with the symmetry group Cn (n) are relatively rare in
ornamental art, the same refers to similarity symmetry rosettes with the
symmetry group CnL (nL). Such similarity symmetry rosettes
occur in enantiomorphic modifications. If the angle of the dilative
rotation L is a rational one, polar radial rays exist. Then, the
existence of a dilatation as the element of the symmetry group CnL
(nL) makes it possible to divide the corresponding similarity symmetry
rosette into the sectors of the dilatation.
Similarity symmetry rosettes with the symmetry group CnL
(nL) (Figure 3.9b, 3.11c, e) possessing a very high degree of visual
dynamism, caused by the polarity of both the relevant components
- n-fold rotation and dilative rotation L - produce a
visual impression of centrifugal rotational expansion. The
existence of models in nature, the dynamic visual impression that
suggest, their expressiveness and visual-symbolic function
resulted in the appearance and use of similarity symmetry
rosettes with the symmetry group CnL (nL) in
ornamental art.

Figure 3.11
|
Examples of similarity symmetry rosettes in Greek and Byzantine
ornamental art.
|
Similarity symmetry groups of the subtype
CnL2n(k,p/n) (nL2n(k,p/n)) can be
derived by desymmetrizations of similarity symmetry groups of the
type DnL (nmL), which are more frequent in
ornamental art. By choosing an appropriate desymmetrization and
eliminating reflections of the symmetry group DnL (
nmL), the symmetry group CnL2n (nL2n) can
be obtained. By the antisymmetry desymmetrization of the symmetry
group DnL (nmL ), the antisymmetry group
DnL/CnL2n (nmL/nL2n), treated by
the classical theory of symmetry as the symmetry group
CnL2n (nL2n) belonging to the type CnL
(nL), can be derived (Figure 3.12b).

Figure 3.12
|
Examples of similarity symmetry rosettes in Roman ornaments.
|
Every symmetry group of the type DnL (nmL) is the
composition of the symmetry groups L(k,p/n) and Dn (
nm) with the same invariant point. A fundamental region of the symmetry
group DnL (nmL) is the section of fundamental regions of these
two symmetry groups. Similarity symmetry rosettes with the symmetry group
DnL (nmL) (Figure 3.9c, d, 3.12c, 3.13) can be constructed
multiplying by the dilative rotation L a rosette with the symmetry group
Dn (nm), belonging to a fundamental region of the symmetry
group L, where the rosette center and the dilative rotation center
coincide. Construction methods used for obtaining similarity symmetry
rosettes with the symmetry group DnL (nmL) are analogous to the
construction methods previously
discussed, used with similarity symmetry groups of the type CnL (
nL). Owing to a very high degree of symmetry, the existence of models in
nature (e.g., flowers and the fruits of certain plants) and frequent
applications of the symmetry group of rosettes Dn (nm), the
type DnL (nmL), regarded from the point of view of ornamental
art, is one of the largest and most heterogeneous types of the similarity
symmetry groups of rosettes S20. For n - an even natural number,
there is no difference between individual symmetry groups of the type
DnL (nmL), depending on the sign of the dilatation coefficient k,
but for n - an odd natural number and k < 0, the relationship
DnL=DnL(k,p/n) = DnK(|k|) = DnK holds.
According to this relationship and the relationship DnK=DnL,
holding for n - an odd natural number and k < 0, the types DnK
(nmK) and DnL (nmL) are dual with respect to the change
of the sign of the coefficient k. Owing to a rational angle of dilative
rotation L, q = p/n, there are the polar radial rays - the axes
of the dilatation K(k2), incident to the reflection lines. Therefore, it
is possible to divide a similarity symmetry rosette with the symmetry group
DnL (nmL) into the sectors of the dilatation. Enantiomorphic
modifications do not exist.

Figure 3.13
|
Examples of Roman floor mosaics with the similarity symmetry groups of the
type DnL (nmL).
|
A similarity symmetry rosette with the symmetry group DnL
(nmL) can be simply derived from a similarity symmetry rosette with
the symmetry group DnK (nmK) by its "centering" - by rotating
every second set of its fundamental regions, homologous regarding
transformations of its subgroup Dn (nm), through the angle
q = p/n. The symmetry group DnL (nmL) can be derived
also by a desymmetrization of the symmetry group DnK (nmK).
Since the symmetry group DnL (nmL) is the subgroup of the index
2 of the symmetry group DnK (nmK), by using the antisymmetry
desymmetrization, the antisymmetry group DnK/
DnL (nmK/nmL), treated by the classical theory of
symmetry as the symmetry group DnL (nmL), can be
obtained.
Similarity symmetry rosettes with the symmetry group DnL
(nmL) possess a specific unity of visual dynamism and stationariness,
produced, respectively, by the dynamic component - dilative
rotation L - and by the static component - subgroup
Dn (nm). The reflections of this subgroup cause the
non-polarity of rotations and alleviate the dynamic visual effect
produced by the dilative rotation L, which suggests an
impression of centrifugal expansion. Changes of the shape of a
fundamental region, which influences the visual impression, in
similarity symmetry groups of the type DnL (nmL)
are restricted to the possible use of curvilinear boundaries,
which do not belong to reflection lines. The other boundaries
must be rectilinear. In all the similarity symmetry groups
containing dilative rotations, a degree of visual dynamism or
stationariness can vary according to the choice of parameters
k, q... The spectrum of possibilities includes
different varieties. This range from visually dynamic similarity
symmetry rosettes with the symmetry group CnL (
nL), with an irrational angle of the dilative rotation L, to
similarity symmetry rosettes with a rational angle, which offer a
perception of the sectors of dilatation, through to static
similarity symmetry rosettes with the symmetry group DnL
(nmL), with the coefficient of dilative rotation
k » 1, which are, by their visual properties, similar to rosettes
with the symmetry group Dn (nm).
The simplest among similarity symmetry groups of the type
CnM (nM) (Figure 3.14, 3.15) is the symmetry group
M (n = 1) generated by the dilative reflection M - a
composite transformation representing the commutative product of
a dilatation and reflection. A fundamental region of the
symmetry group M is a part of the plane defined by two
homologous lines of the dilative reflection M. The polar
radial rays exist. Due to the presence of the indirect
transformation - dilative reflection M - there is no the
possibility of the enantiomorphism.

Figure 3.14
|
The rosette with the similarity symmetry group C4M (4M) in the
ornamental art of Oceania, Bali.
|

Figure 3.15
|
Examples of similarity symmetry rosettes in the ornamental art of
Oceania (New Zealand, New Guinea, Solomon Islands).
|
There are several ways to construct figures with the similarity
symmetry group M. They can be divided into non-metric constructions,
based on the use of the non-metric properties of the dilatation
K - parallelism or antiparallelism of homologous vectors of
the dilatation K, equiformity, equiangularity and linking of
its successive homologous asymmetric figures - and metric
constructions, based on the use of the metric property of the
dilatation K that is a constitutive part of the composite
transformation M(k,m). Such a construction always begins
with the metric construction of a series of homologous asymmetric
figures of the dilatation K. After that, it is necessary to
copy by the reflection in the reflection line m, every
second homologous figure mentioned. Combinations of these methods
are also possible.
For the needs of ornamental art, probably the most efficient is the
non-metric construction, consisting of the construction of a series of
asymmetric figures that satisfy the dilatation K(|k|), by
applying the linking of successive homologous asymmetric figures of the
dilatation K. After that, every second figure must be copied by the
reflection with the reflection line m for k > 0, or by the reflection
with the reflection line m' perpendicular to the reflection line
m in the invariant point for k < 0. In line with this, when analyzing the
similarity symmetry group M, it is not necessary to discern the cases
of k > 0, k < 0.
By applying the metric construction method, aiming for maximal
constructional simplicity, there frequently occur deviations from the
requirements of similarity symmetry. In such a case, the geometric
progression mentioned above, is replaced by an analogous arithmetic
progression.
Since a dilative reflection is present in nature (e.g., in the
arrangement and growth of leaves in certain plants), natural models are
imitated by ornamental art. Therefore, the similarity symmetry group M
appears even in Paleolithic ornamental art, although followed by deviations
with respect to the geometric consistency. The other reason for the origin
and the use of the similarity symmetry group M can be found in the
visual effect and symbolic meanings which corresponding similarity symmetry
rosettes possess. Owing to the polarity of the radial ray incident to the
reflection line m and due to the dynamic visual properties of the
dilative reflection, similar to that of a glide reflection, figures with the
symmetry group M can serve as the visual symbols of oriented, polar
alternating phenomena of a growing intensity. It is, probably,
the origin and reason for the frequent occurrence of similarity
symmetry rosettes with the symmetry group M in primitive
art. They occurr independently, or within more complex similarity
symmetry rosettes with a symmetry group of the type CnM
(nM) (Figure 3.14, 3.15). By varying the dilatation
coefficient k and the angle between the reflection line m
and the radial ray of the dilatation K(k2) which belongs to
the symmetry group M and generates its subgroup of the
index 2, it is possible to emphasize or alleviate the dynamic
visual effect produced by the polar radial ray, which goes from
suggesting an impression of dynamism, similar to that produced
by a glide reflection, to an impression of stationariness similar
to that produced by a reflection.
The use of the similarity symmetry group M in painting, comes
to its full expression when presenting objects with the symmetry group
1g by applying the central perspective.
Similar characteristics of all the similarity symmetry groups of
the type CnM (nM) are conditioned by the essential properties
of the similarity symmetry group M. Similarity symmetry groups of the
type CnM (nM) are the result obtained when composing the
symmetry groups M and Cn (n) with the same invariant
point. Similarity symmetry rosettes with the symmetry group CnM (
nM) can be constructed by multiplying by the n-fold rotation a
figure with the similarity symmetry group M, belonging to a
fundamental region of the symmetry group Cn (n),
or multiplying by the dilative reflection M a figure with the
symmetry group Cn (n), belonging to a fundamental
region of the symmetry group Cn (n). In both
cases the rosette center and the dilative reflection center
must coincide. The application of the non-metric construction
method, combined with the use of the linking of asymmetric
homologous figures of the dilative reflection M, is also
possible. With the use of the metric construction method there
often occur deviations from the regularities of the similarity
symmetry group M - the replacement of the geometric
progression mentioned above with a corresponding arithmetic
progression, the disturbance of equiformity and equiangularity,
and, consequently, of the similarity symmetry. These deviations
are the result aiming for maximal constructional simplicity.
A fundamental region of the symmetry group CnM (nM) is
the section of fundamental regions of the symmetry groups Cn (
n) and M with the same invariant point. Within the type CnM
(nM), there will be no essential differences between individual
symmetry groups, caused by the sign of the dilatation coefficient k. Every
symmetry group CnM(k,m), for n - an odd natural number
and k < 0, can be treated as the symmetry group CnM(|k|,
m'), where by m' is denoted the reflection line perpendicular in the
invariant point of the dilative reflection M(k,m) to the reflection
line m. Hence, for n - an odd natural number and k < 0, the
relationship CnM(k,m)=CnM(k,m') holds.
Similarity symmetry rosettes with the symmetry groups
CnM(k,m) and CnM(-k,m) will differ
between themselves regarding the position of the dilative
reflection axis, only for n - an odd natural number, while
for n - an even natural number, there will be no such
difference. There are no enantiomorphic modifications.
Reasons for the appearance and the use of similarity symmetry
rosettes with the symmetry group CnM (nM) in ornamental art,
can be found in the imitation of natural forms, in certain arrangements of
leaves and in the growth of some plants, combined with a decorative effect
of rosettes with the symmetry group Cn (n). Among all
similarity symmetry rosettes, those with similarity symmetry groups of the
type CnM (nM) possess the maximal degree of visual dynamism,
conditioned by two dynamic components - the n-fold rotation and dilative
reflection M, which combines by itself the visual dynamism of alternating
motion and that of centrifugal expansion, caused by its dilative component.
The intensity of the dynamic visual effect can be influenced by choosing the
parameter k and the position of the reflection line m.
The symmetry groups Cn (n) and M are relatively
rare in ornamental art. The same refers to the similarity symmetry groups of
the type CnM (nM), formed as their compositions. A similarity
symmetry group CnM (nM) can be obtained also by a
desymmetrization of the symmetry group DnK (nmK) or DnL
(nmL), examples of which are, due to their higher degree of symmetry,
visual and constructional simplicity, more frequent in ornamental art.
Desymmetrizations achieved by a dichromatic coloring often result in
antisymmetry groups of the type DnK/CnM (
nmK/nM) or DnL/CnM (nmL/nM),
which in the classical theory of symmetry are considered within
the type CnM (nM). The same can be realized by
suitable classical-symmetry desymmetrizations.
Similarity symmetry groups of the type DnM (nmM), the
existence of which was proposed by A.V. Shubnikov (1960), coincide to the
similarity symmetry groups of the type DnL (nm).
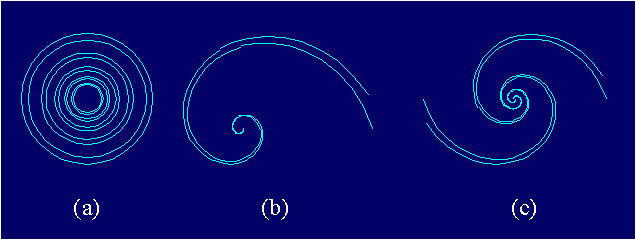
Among the continuous similarity symmetry groups of rosettes
S20, the symmetry groups D¥ K (¥mK) and
CnL1 (nL1) will have adequate visual interpretations, without
using textures (Figure 3.5). As a visual model of the symmetry group
D¥ K (¥mK), a series of concentric circles
can be used - this model being obtained multiplying by the
dilatation K two different concentric circles with the center
incident with the dilatation center.
Adequate visual interpretations of all the other continuous
similarity symmetry groups can be obtained only by using
textures - the average even density of some elementary
asymmetric figure, arranged according to the given continuous
symmetry group. Concerning physical interpretations, all the
continuous similarity symmetry groups have adequate
interpretations, which can be realized by using physical factors
(e.g., motion, rotation, the effect of a physical field, etc.).
*
*
*
The central problem with the similarity symmetry groups of rosettes
S20 and their examples in ornamental art is the question of the
construction of corresponding similarity symmetry rosettes. As basic
construction methods, it is possible to distinguish, first, the non-metric
method, based, directly or indirectly, on the parallelism of homologous
asymmetric figures of a dilatation, their equiangularity and equiformity;
second, the metric method, founded on the fact that the distances of
homologous points of the similarity transformations K, L, M from the
invariant point form a geometric progression; and, third, combinations of
these methods.
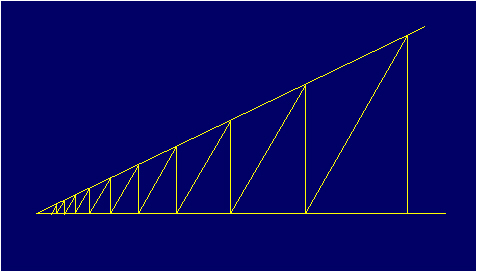
The non-metric construction method gives the best results,
guaranteeing that equiformity and equiangularity will be respected, and may
serve for the direct construction of similarity symmetry rosettes of the
type CnK (nK) or DnK (nmK) with the dilatation
coefficient k > 0, by applying the linking of successive homologous
asymmetric figures of the dilatation K or dilative reflection M (Figure
3.3, according to A.V. Shubnikov, 1960). In the other cases, when similarity
symmetry transformations are composite transformations, this means, in
symmetry groups of the types CnK (nK), DnK (nmK)
with k < 0, and all the symmetry groups of the types CnL (nL),
DnL (nmL), CnM (nM), it is not possible to use
exclusively linking and parallelism. In these cases, after the first part of
the construction, the copying of successive homologous asymmetric figures of
the dilatation K (k > 0) by means of corresponding rotations and
reflections becomes indispensable, so the construction becomes more
complicated. In those cases where is not possible to link homologous
asymmetric figures of a dilatation, because of the complexity of
construction, the non-metric method has a relatively limited application.
The metric construction method shows its superiority, in the sense
of constructional simplicity, in those situations when the non-metric
construction method is difficult to apply - with composite similarity
transformations or with unlinked homologous asymmetric figures obtained by
dilatation. A negative aspect of the metric construction method, coming to
its expression in ornamental art, is the possibility for replacing the
geometric progression mentioned above by a corresponding
arithmetic progression, aiming for maximal constructional
simplicity. Such an inconsistent application of the metric
construction method unavoidably disturbs the equiangularity,
equiformity, and consequently, the similarity symmetry.
In ornamental art we can find many similarity symmetry rosettes,
formed by the inconsistent use of the construction methods mentioned. Such
rosettes do not satisfy the similarity symmetry but only suggest it. In
early ornamental art, this is not the exception but the rule.
Both construction methods mentioned are used to construct
similarity symmetry rosettes, formed by applying the similarity
transformations K, L, M on a rosette with the symmetry group Cn
(n) or Dn (nm) belonging to a fundamental region of the
corresponding similarity symmetry group K, L or M. An
opposite approach - the multiplication of a figure with the similarity
symmetry group K, L, M, by the symmetries of the symmetry
group Cn (n) or Dn (nm) - is not so frequent.
Such a construction requires a better understanding of the similarity
symmetry, especially concerning the fundamental regions of the generating
groups, to avoid the possible overlapping of figures. In all those cases,
the generating symmetry group of rosettes and the similarity symmetry group
possess the same invariant point.
The desymmetrization method is not an independent construction
method. It can be used exclusively if we know similarity symmetry groups of
rosettes with a higher degree of symmetry, which can be reduced to a lower
degree of symmetry by the elimination of certain symmetry elements, to
derive their similarity symmetry subgroups. However, since similarity
symmetry groups of a higher degree of symmetry, due to the principle of
visual entropy, are more frequent and much older, this construction method
has been abundantly used in ornamental art, with the classical-symmetry,
antisymmetry and color-symmetry desymmetrizations.
Like the antisymmetry and colored symmetry groups of rosettes,
friezes and ornaments, such desymmetrizations of similarity symmetry groups
are of a somewhat later date, appearing in ornamental art with dichromatic
and polychromatic ceramics (in the Neolithic and in the period of the
ancient civilizations). Classical-symmetry desymmetrizations can be used to
derive similarity symmetry subgroups of the arbitrary index of the given
similarity symmetry group. Desymmetrizations of the continuous visually
presentable similarity symmetry groups of the type D
¥K (¥mK), which can be visually interpreted by a
system of concentric circles, obtained from two different
concentric circles multiplied by the dilatation K with the same
center, frequently occur (Figure 3.5a). This continuous
similarity symmetry group is a perfect basis on which to apply
the desymmetrization method. Continuous similarity symmetry
groups of the type CnL1 (nL1) (Figure 3.5b, c)
are based on the continuous visually presentable conformal
symmetry group L1ZI, which can be visually
interpreted by the corresponding logarithmic spiral. Therefore,
they make possible a very simple transition from the visually
presentable continuous, to the corresponding discrete similarity
symmetry groups.
The classical-symmetry desymmetrization method can be very
successfully applied on the similarity symmetry groups generated by the
symmetry group Dn (nm), to obtain their subgroups, generated
by the symmetry group Cn (n). Since the symmetry group
Cn (n) is the subgroup of the index 2 of the symmetry group
Dn (nm), there is a possibility for antisymmetry desymmetrizations.
More detailed information on possible desymmetrizations of
similarity symmetry groups can be found in the table of the group-subgroup
relations existing between different types of the similarity symmetry
groups of rosettes, and in the tables of antisymmetry and color-symmetry
desymmetrizations.
Since the continuous similarity symmetry groups
D¥K (¥mK) and CnL1 (
nL1) are visually presentable, very important are the
group-subgroup relations between the continuous and discrete
similarity symmetry groups of rosettes S20: D¥K
® DK, DL, CL1 ®
CL. Between the different types of discrete similarity symmetry
groups, the following relations hold: DL ®
DK ® CM ® CK, using
the symbols D, C instead of the symbols Dn,
Cn, for denoting the group-subgroup relations between
the types, and not between the individual symmetry groups.
When establishing the group-subgroup relations between the
individual similarity symmetry groups of rosettes S20 and their
subgroups, we can use the group-subgroup relations existing between the
symmetry groups Cn (n), Dn (nm) and the
group-subgroup relations between the symmetry groups K, L,
M, since all the similarity symmetry groups of rosettes S20 are
derived as the superpositions of the symmetry groups mentioned, i.e. as the
extensions of the symmetry groups of rosettes G20: Cn (n),
Dn (nm) by the similarity transformations K, L, M. For
the discrete similarity symmetry groups K, L, M, the
following relationships hold: [K:K(km)] = m, [M:
M(km)] = m, [L:L(km,kq)] = m (m Î N). For a
rational angle of the dilative rotation
q = pp/q, (p,q) = 1, p,q Î Z, the following relationships hold: [L:L(kq,qq)] = q
and L (kq,qq) = L((-1)pkq,0) = K((-1)pkq),
showing that every symmetry group L with a rational angle of dilative
rotation q contains the subgroup generated by the dilatation
K((-1)pkq). The relationship [M:K(k2)] = 2 highlights the
existence of the subgroup of the index 2 generated by the dilatation
K(k2) in every symmetry group M, while the relationship
CnK=CnL(k,0) = CnL0 highlights the different type
possibilities for the symmetry groups CnK (nK). This means that
they can be discussed within the type CnL (nL), as the subtype
CnL0 (nL0).
By accepting the criterion of subordination, by treating the
symmetry group K within the type CnL (in accordance with the
relationship K=L0), and the type CnK (nK) as the
subtype of the type CnL (nL) (in accordance with the
relationship CnK=CnL0), the whole discussion on the discrete
similarity symmetry groups of rosettes can be reduced to the analysis of
the symmetry groups of the types CnL (nL), CnM (
nM), DnK (nmK) and DnL (nmL). The criterion of
the maximal symmetry can be introduced even between individual symmetry
groups of the type CnL (nL), where the symmetrization caused by
a superposition of the n-fold rotation and the rotational component of the
dilative rotation L results in the change of the minimal angle of the
dilative rotation, and in the appearance of the new dilative rotation L',
i.e. in the new symmetry group CnL' (nL').
In the table of antisymmetry desymmetrizations of discrete
similarity symmetry groups of rosettes, the symbols of antisymmetry groups,
i.e. the corresponding antisymmetry desymmetrizations, are given in the
group/subgroup notation G/H. The symbol q' corresponds to a newly
derived minimal angle of the dilative rotation L'.
The table of antisymmetry desymmetrizations of similarity symmetry groups of
rosettes S20:
|
CnK/CnK | CnM/CnK
|
|
C2nK/CnK | C2nM/CnM
|
|
C2nK/CnL2n
|
|
| CnL/CnL(k2,2q)
|
|
DnK/DnK | C2nL/CnL
|
|
DnK/CnM | CnL/CnL'(k,q')
|
|
DnK/CnK
|
|
D2nK/DnK | DnL/DnK
|
|
D2nK/CnL2n | DnL/CnL2n
|
|
| DnL/CnM
|
|
Besides the possibilities to apply the antisymmetry
desymmetrization method, this table gives evidence for all the
subgroups of the index 2 of any given discrete similarity
symmetry group of rosettes. By using data given by A.M. Zamorzaev
(1976), it is possible to compare similarity antisymmetry groups
with the corresponding crystallographic antisymmetry groups of
polar, oriented rods G31. A complete catalogue of the
similarity antisymmetry groups of rosettes S20' is given by
S.V. Jablan (1986b).
The color-symmetry desymmetrizations of the discrete
crystallographic similarity symmetry groups of rosettes can be partially
considered by using the work of E.I. Galyarski (1970, 1974b),
A.M. Zamorzaev, E.I. Galyarski, A.F. Palistrant (1978),
and A.F. Palistrant (1980c).
Different problems of tiling theory (B. Grünbaum, G.C. Shephard,
1987) are extended to the similarity symmetry groups of rosettes S20 by
E.A. Zamorzaeva (1979, 1984). In the works mentioned, a link is established
between the similarity symmetry groups of rosettes S20, the symmetry
groups of polar oriented rods G31 and corresponding symmetry groups of
ornaments G2, resulting in the following relationships: CnK (
nK), CnL (nL) @ p1, CnM ( nM)
@ pg, DnK (nmK) @ pm, DnL
(nmL) @ cm. In this way, different problems of
similarity symmetry plane tilings are reduced to the much better known
problems of tilings that correspond to the symmetry groups of ornaments
p1, pg, pm, cm. By using such an approach, the problems
of isohedral and 2-homeohedral similarity symmetry plane tilings are solved
by E.A. Zamorzaeva.
The chronology of similarity symmetry rosettes in ornamental art is
connected with the problem of their construction. The oldest examples of
rosettes suggesting similarity symmetry date to the Paleolithic and
Neolithic, beginning with the appearance of the first spiral forms in art
(Figure 3.7), series of concentric circles or concentric squares with
parallel sides, and motifs based on natural models with the similarity
symmetry group M or D1K (mK), etc. In the Neolithic we
come across more diverse and complex examples of rosettes with similarity
symmetry groups of the type CnL (nL) or DnL (nmL)
(Figure 3.9). Already in the Neolithic and in the ornamental art of ancient
civilizations, there are examples of all the types of similarity symmetry
groups of rosettes. Though, almost unavoidably, there are deviations from
geometric regularity, these being due to the approximate constructions used
in ornamental art. Ornamental motifs with the application of similarity
symmetry reached their peak in the ornamental art of Rome and Byzantium
(Figure 3.11-3.13), mainly in floor mosaics. Here we find examples of all
the types of the similarity symmetry groups of rosettes, without any
deviations from strict geometric regularity.
One of the conditions necessary for the appearance of corresponding
similarity symmetry rosettes in ornamental art is the existence of models in
nature, i.e. a spiral tendency in nature, expressed through the way of
growth of certain living beings or as a result of rotational motions (e.g.,
whirlpools in a turbulent fluid motion, etc.). In the earlier periods of
ornamental art, it is possible to note the imitation of models in nature
that possess similarity symmetry. In the further development of ornamental
art, a visual-symbolic component based on a suggestion of the impression of
centrifugal expansion, produced by similarity symmetry rosettes, became the
main reason for the use of similarity symmetry. After empirically solving
the construction problems and discovering all the symmetry
possibilities, i.e. all the types of the similarity symmetry groups of
rosettes, primary symbolic meanings retreated into a concern for
decorativeness. That opened new possibilities for the
enrichment and variety of similarity symmetry rosettes in
ornamental art.
Like with the symmetry groups of rosettes G20, where rosettes
with the symmetry groups of the type Dn (nm) are more frequent
than rosettes with the symmetry groups of the type Cn (n), the
principle of visual entropy and numerous models in nature caused the
dominance of rosettes with similarity symmetry groups of the type DnK
(nmK), DnL (nmL), over those with similarity symmetry
groups of the types CnK (nK), CnM (nM),
CnL (nL). As generating symmetry groups of the type Dn (
nm), most frequently are used symmetry groups of rosettes
D1 (m), D2 (2m), D4 (4m),
D6 (6m), etc., mainly with n - an even natural
number. In such rosettes the incidence of reflection lines to the
fundamental natural directions - vertical and horizontal line
- is possible.
A fundamental region of similarity symmetry groups offers the
variation and the use of curvilinear boundaries. Rectilinear must be only
those parts of the boundaries of the fundamental region that coincide with
reflection lines. By changing the form of a fundamental region we can
influence the intensity of static or dynamic visual impression produced by
the given similarity symmetry rosette and intensify desired visual
impression. In all similarity symmetry rosettes, it is possible to realize
the corresponding (unmarked) isohedral plane tilings.
A basic visual property of similarity symmetry rosettes is the
impression of centrifugal expansion, which these rosettes render to the
observer. The intensity of that impression will depend primarily on the
value of the coefficient k, on the form of a fundamental region or an
elementary asymmetric figure belonging to the fundamental region, where the
adequate use of acuteangular forms may stress a dynamic effect of a
dilatation, occurring as the independent or dependent symmetry
transformation. Polar, oriented rotations existing in subgroups of the type
Cn (n) play the role of visual dynamic symmetry elements.
Dilative reflections have a double, contradictory role, since they cause the
absence of the enantiomorphism in groups of the type CnM (nM).
On the other hand, they increase visual dynamism, by suggesting the
impression of a centrifugal alternating expansion. By varying the parameter
k and the position of the reflection line m, we can stress the
visual static or dynamic function of the dilative reflection
M(k,m).
Enantiomorphic modifications do not exist in similarity symmetry
groups of the types CnM (nM), DnK (nmK),
DnL (nmL), D¥K (¥mK), i.e. in groups
containing at least one indirect symmetry transformation. The presence of
the dilatation K or K(k2) is obligatory in all the similarity symmetry
groups of rosettes, except groups of the type CnL (nL),
which contain a dilatation only when the angle of the dilative rotation L
is rational. Then is possible to perceive sectors of dilatation. Since the
presence of a dilatation within the symmetry group CnL (nL)
increases the number of different symmetry transformations and simplifies
the construction of corresponding rosettes, in line with the principle of
visual entropy, similarity symmetry groups of the type CnL (
nL), offering a division of the corresponding similarity symmetry rosettes
into sectors of dilatation, will be more frequent in ornamental art than
groups of the type CnL (nL) with an irrational angle of the
dilative rotation L.
Because of a high degree of symmetry and the possibility for the
simple construction of their corresponding visual interpretations by
desymmetrizations of groups of the type D¥K (
¥mK), of special interest will be groups of the types
DnK (nmK) or DnL (nmL). According
to the principle of visual entropy, similarity symmetry groups
generated by the symmetry groups of rosettes of the type
Dn (nm), for n = 1,2,3,4,6,8,12,..., are the oldest
and most frequent in ornamental art. In visual interpretations
of the derived similarity symmetry groups of rosettes a dynamic
visual component - the suggestion of a centrifugal expansion
conditioned by dilatation - is in visual balance with the
static component produced by reflections. The result is
non-polarity of rotations and absence of the enantiomorphism. On
the other hand, in the older ornamental art and that of primitive
people, visually dynamic rosettes with similarity symmetry groups
of the types CnK (nK), CnL (nL),
CnM (nM), CnL1 (nL1), with
polar rotations and dilative reflections, are very frequent.
Their abundant use in ornamental art, is due to their symbolic
function.
Besides serving as a basis for the application of the
desymmetrization method, the tables of the group-subgroup relations between
the types of similarity symmetry groups or between the individual groups
are, at the same time, an indicator of symmetry substructures of a given
similarity symmetry group. They represent the groundwork for the exact
registering of the subentities mentioned, which with an empirical
visual-perceptive approach is sometimes very difficult. The surveys given
consist of a series of inclusion relations beginning with the maximal
visually presentable continuous similarity symmetry groups of the types
D¥K (¥mK) and CnL1 (nL1), including all
discrete similarity symmetry groups and ending with the symmetry groups of
rosettes Dn (nm) and Cn (n) and their subgroups.
When discussing continuous similarity symmetry groups, only the visually
presentable groups are considered, since ornamental art imposes
this restriction. Visually non-presentable similarity symmetry
groups will have their physical interpretations, owing to the
possibility of including physical desymmetrization factors (e.g.,
a uniform rotation of a rosette with the similarity symmetry
group D¥K (¥mK) around the invariant
point, when its symmetry group is reduced to the symmetry group
C¥ K (¥K), or by using similar
methods). In ornamental art, visual presentations of such
continuous similarity symmetry groups can be obtained by using
textures. As physical interpretations of these groups, we may
consider different similarity symmetry structures realized by
means of a physical field with a singular point, the intensity of
which depends on distance from the singular point, according to
the requirements of the similarity symmetry.
In analyzing the visual properties of similarity symmetry groups we
can use, very efficiently, their visual interpretations: similarity symmetry
rosettes, tables of the graphic symbols of symmetry elements and Cayley
diagrams. Owing to the existence of the isomorphism between the similarity
symmetry groups of rosettes S20 and the symmetry groups of polar,
oriented rods G31, the properties of the similarity symmetry groups of
rosettes S20, the characteristics of similarity transformations and
relations which are included in their presentations, will be, sometimes,
more evident in the symmetry groups of polar, oriented rods G31.
The symmetry groups of rods G31, that in the isomorphism mentioned
correspond to the similarity symmetry groups of rosettes S20, possess
the same presentations and geometric characteristics. By analyzing the
symmetry groups of rods G31, the conclusion on the absence of the type
DnM (nmM) of the similarity symmetry groups of rosettes and
its reduction to the type DnL (nmL), becomes absolutely
clear. The same is proved by the table of the symmetry groups of rods
G31 (A.V.Shubnikov, V.A.Koptsik, 1974) in which, because of the
justification already given, there is no individual type (
a)(2n)nã, consisting of groups isomorphic to
similarity symmetry groups of the type DnM
(nmM) .
These symmetry groups of rods are included in the type (a)(2n)nm, consisting of groups isomorphic to the
similarity symmetry groups of the type DnL (nmL).
The problem of plane symmetry groups isomorphic to the symmetry
groups of non-polar rods G31 is solved in the theory of conformal
symmetry introduced by A.M. Zamorzaev, E.I. Galyarski and A.F. Palistrant
(1978), in the Euclidean plane with a singular point O removed, i.e. in
the plane E2\{O} .
All the other problems in the field of visual interpretations of the
similarity symmetry groups of rosettes S20 - "objective" and
"subjective" symmetry, problems of perceiving the objective symmetry and
eliminating other visual symmetry factors, desymmetrizations or
symmetrizations caused by physiological-physical reasons, the effect of the
principle of visual entropy, problems of visual perception of substructures,
treatment of symmetry groups of "real" similarity symmetry rosettes as
finite factor groups of "ideal", infinite similarity symmetry groups of
rosettes, etc. - can be discussed analogously to the similar problems of
visual perception previously analyzed with the symmetry groups of rosettes
G20, friezes G21 and ornaments G2.
The chronological parallelism and the use of similar construction methods
in ornamental art and the theory of similarity symmetry, the more profound
connection between the similarity symmetry groups used in ornamental art and
the theory of symmetry, the possibility of a different approach to
ornaments treating them as models of geometric-algebraic structures and many
other similar questions, are some of the problems raised in this work that
demand a more detailed study.