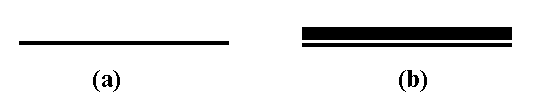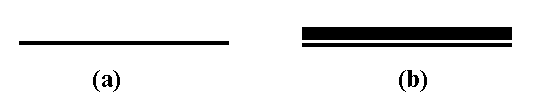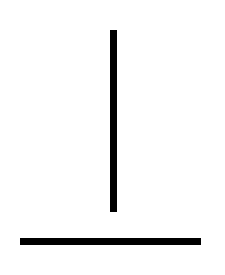continuous translation axis and the
continuous symmetry group p01m (0m). The
phenomenon of a visual, subjective desymmetrization of a vertical
line is probably implied by gravitation. It is possible that
the tendency of a vertical line to go upward results from the
objective narrowing of vertical objects in the upper part; from
the visual convergence of parallel lines with high objects
observed from a lower position; and from the habit conditioned
by a constant application of the central perspective, where the
center of the perspective is usually placed in the upper part of
the picture. A vertical line has the "directed tension", so that
along with the objective symmetry m0m, occurs its
visual, subjective desymmetrization and the reduction to the
symmetry 0m. The tendency to accept a vertical form as
longer in comparison with the horizontal form of the same length
is conditioned by the polarity of the vertical axis (Figure
2.30).
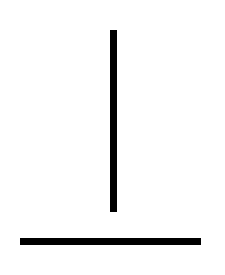
Figure 2.30
|
Illustration of the visual effect of polarity of the vertical
line (the vertical and horizontal line segments are of the same
length).
|
A similar visual, subjective desymmetrization - a
reduction to a lower degree of symmetry and the polarity of the
axis - occurs also with an "ascending" and "descending"
diagonal. This phenomenon can be also treated as the difference
between the "right" and "left" (H. Weyl, 1952, pp. 16;
R. Arnheim, 1965, pp. 22), in the theory of visual perception
discussed by H. Wölfflin, M. Gaffron, A. Dean and S. Cobb.
Along with different physiological interpretations, there is an
interesting Weyl's question about whether this phenomenon is
connected to writing from the left to right, and whether it is
expressed by nations writing in the opposite direction. M.Gaffron
tried to explain it by the dominance of the left brain cortex
containing brain centers for several activities in right-handed
people, i.e. in the dominance of righthandness. About this,
S. Cobb says (R. Arnheim, 1965,
pp. 23): "Many fanciful ideas have
been put forward, from the theory that the left hemisphere has a
better blood supply than the right, to the heliocentric theory
that the right hand dominates because man originated north of the
equator and, looking at the sun, was impressed with the fact that
great things move toward the right! Thus right became the symbol
of rectitude and dexterity, and things on the left were sinister.
It is an interesting observation that about 70 per cent of human
foetuses lie in the uterus in the "left occiput posterior"
position, i.e. facing to the right. No one has ever found out
whether or not these become the right majority of babies.
Probably the dominance of right-handness is due to chance in
heredity.".
All the continuous symmetry groups of friezes have
physical interpretations (A.V. Shubnikov, V.A. Koptsik, 1974). In
the visual arts, besides visual models of the continuous symmetry
groups of friezes m01 and m0m (Figure 2.29)
with the non-polar translation axis, adequate visual
interpretations of the other continuous symmetry groups of
friezes with the polar or bipolar translation axis, can be
realized, in the sense of the objective symmetry, exclusively by
textures. Textures can be realized by equal average density of
the same asymmetric elementary figures arranged along the
singular direction in accordance with the corresponding
continuous symmetry group. For a schematic visual interpretation
of these groups by using the graphic symbols of symmetry
elements, certain supplementary symbols (e.g., arrows) are
indispensable (B. Grünbaum, G.C. Shephard, 1987).
The oldest examples of friezes are found in the art of
the Paleolithic (Magdalenian, 12000-10000 B.C.) and Neolithic.
In fact, examples of all seven discrete and two visually
presentable symmetry groups of friezes are known from the
Magdalenian period.
Despite a relative variety of motifs in ornamental
art, there is also a repetition of ornamental motifs - basic,
elementary patterns occurring in different parts of Europe, Asia
and Africa, where the late Paleolithic and Neolithic cultures
were formed. Since the possibilities for communication between
distant areas were remote, we can assume that common ornamental
motifs result from similar or the same models found in nature by
prehistoric peoples and from the laws of symmetry.
Most frequently, friezes are the result of a translational
repetition of different motifs, where the symmetry of the
original motif - a rosette - determines the symmetry of the
frieze itself, in the sense of composition of the translational
group 11 and the symmetry group of the rosette or by an
artistic schematization of natural objects possessing by
themselves the symmetry of friezes.
The origins of friezes are visible in cave drawings and
engravings on stones or bones from the earliest period - late
Paleolithic.
Representing a herd of deer (Figure 2.31), prehistoric
man had abstracted a motif, almost reducing it to a translational
repetition of a pair of horns, i.e. to the frieze with the
symmetry group 11. A similar process, from the motif of
dance to a frieze with the symmetry group m1, from the
motif of harpoon to a frieze with the symmetry group 1m,
from the motif of waves to a frieze with the symmetry group
12 or mg, shows the original symbolic meanings friezes
carried. Thus, friezes became one of the first visual
communication means.

Figure 2.31
|
The origin of friezes with the symmetry group 11 by the
stylization of natural models (Paleolithic, Altamira cave, Spain).
|
Also, the symmetry of friezes based on repetition, have made
possible a symbolic representation of certain periodic natural phenomena -
the turn of day and night, the daily and annual revolving of the Sun -
where friezes played the role of a calendar. This is witnessed by friezes
originating from ethnical art and having even today precisely defined
symbolic meanings and adequate names (Figure 2.54).
The symmetry group of friezes 11 is the result of a
periodic, translational repetition of an asymmetric figure. The form of the
fundamental region can be arbitrary. Owing to the polarity of the frieze
axis and the sheer repetition of the motif, besides a possibility for
figurative representation, there is also a possibility for a
geometric-symbolic representation of directed phenomena. Hence, directed
tension resulting from the polarity of the axis creates an impression of
"motionless motion", thus forming the time component of painting. In
combination with overlapping which makes possible the suggestion of the
perspective in the sense "in front-behind", friezes have been frequently
used in Egyptian art, both decorative and painting, and in the art of
cultures tending to the "objective", natural axonometric presentation of
spatial groups in motion (Figure 2.32-2.35).

Figure 2.32
|
Examples of friezes with the symmetry group 11 in Paleolithic
art.
|

Figure 2.33
|
Examples of friezes with the symmetry group 11 and the formation
of geometric ornamental motifs by stylization and schematization of natural
models (Paleolithic).
|

Figure 2.34
|
Examples of friezes with the symmetry group 11 in Neolithic art
(Hallaf ceramics, around 5500-4500 B.C.).
|
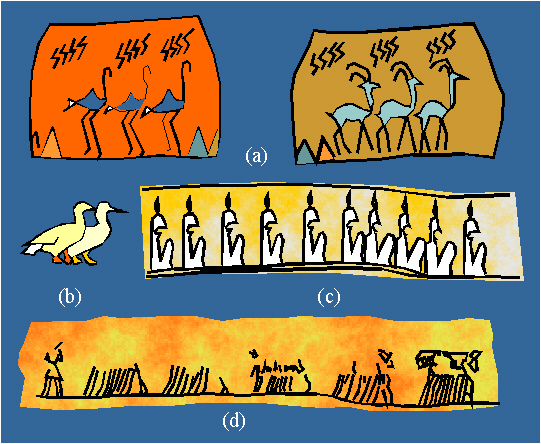
Figure 2.35
|
Examples of friezes with the symmetry group 11 in the art of (a),
(b) pre-dynastic; (c) dynastic period of Egypt.
|
A similar dynamic effect is produced by friezes with the symmetry
groups 1g (Figure 2.36, 2.37) and 1m (Figure
2.38-2.40) which have a polar axis. By using different
elementary asymmetric figures belonging to the fundamental region
and different directed forms with acute angles oriented toward
the direction of the axis, it is possible to intensify the
already existing impression of motion. Owing to their relation to
the growth of certain plants, friezes with the symmetry group
1g hold an important place in plant ornaments (Figure
2.37). Since they contain a glide reflection as the symmetry
element, such friezes are suitable for representing all directed
alternating phenomena or objects by means of geometric ornaments.
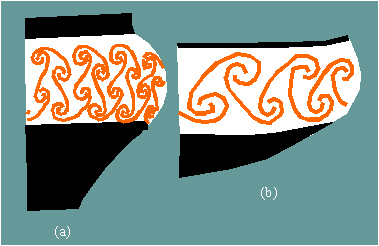
Figure 2.36
|
Examples of friezes with the symmetry group 1g in the Neolithic
art of Yugoslavia: (a) Butmir, around 3500 B.C.; (b) Adriatic zone, around
3000-2000 B.C.
|
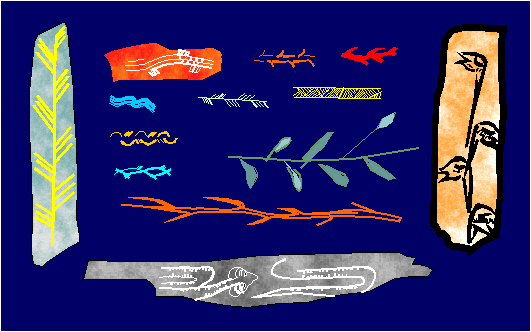
Figure 2.37
|
Examples of friezes with the symmetry group 1g in the art of the
late Paleolithic and early Neolithic (Fontarnaud-Lugasson, Laugerie Haute,
Le Placard, Marsoulas, around 15000-8000 B.C.).
|
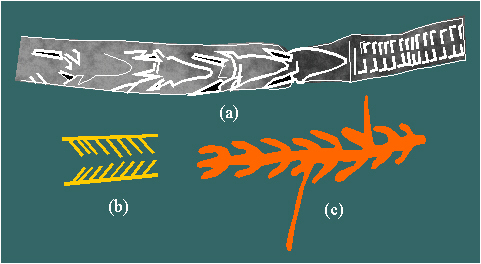
Figure 2.38
|
Examples of friezes with the symmetry group 1m in Paleolithic
art: (a) l'Abri Mege; (b) La Pasiega; (c) Marsoulas.
|

Figure 2.39
|
Friezes with the symmetry group 1m in Paleolithic art (Maz
d'azil, La Madlene, Barma Grande, Laugerie Base, around 10000 B.C.).
|

Figure 2.40
|
Examples of friezes with the symmetry group 1m in Neolithic art,
around 6000-3000 B.C.
|
Owing to the existence of a central reflection as the symmetry
transformation of the group 12, the frieze axis is bipolar, so
friezes with the symmetry group 12 offer the possibility for
registering oppositely directed elementary asymmetric figures along the
singular direction, i.e. two oppositely directed friezes with the symmetry
group 11. Friezes with the symmetry group 12 occur in
many cultures (in the Neolithic, Egyptian, Aegean, etc.), with the
application of spiral motifs (Figure 2.41-2.45).

Figure 2.41
|
Examples of friezes with the symmetry group 12 in Paleolithic and
Neolithic art: (a) Mezin, USSR, around 12000-10000 B.C.; (b), (c) the
Neolithic of Europe; (d), (e) Hacilar, around 5300 B.C.
|
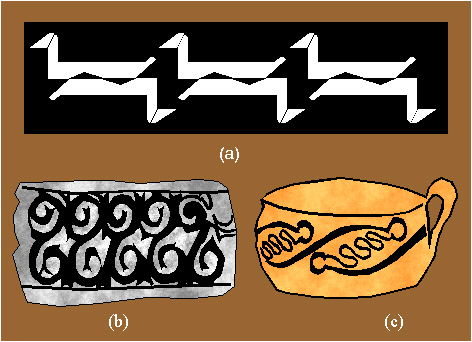
Figure 2.42
|
Examples of friezes with the symmetry group 12: (a) Bakun, Iran,
around 5000-4000 B.C.; (b) Malta, around 3000 B.C.; (c) Crete, around
3000-2500 B.C.
|

Figure 2.43
|
Friezes with the symmetry group 12 in the Neolithic art of
Yugoslavia: (a) Aznabegovo-Vrshnik, around 5000 B.C.; (b) Hvar, around 2500
B.C.
|

Figure 2.44
|
Examples of friezes with the symmetry group 12 in the
pre-Columbian art of America (Mexico).
|

Figure 2.45
|
Friezes with the symmetry group 12 with the application of
spiral motifs: (a) Neolithic art, Butmir, Yugoslavia; (b) Egypt.
|
All the other discrete symmetry groups of friezes m1,
mg, mm and the continuous symmetry groups of friezes
m01 and m0m with the non-polar axis, which contain
reflections with reflection lines perpendicular to the frieze axis, create
an impression of stationariness and balance.
Friezes with the symmetry group m1 were frequently used
in the prehistoric period with the motif of the cult dance "kolo". The
origin and development of this motif can be seen in the stone drawings from
the period of cave painting (Figure 2.46). This motif, very characteristic
and suitable for the analysis of the history of ornamental art, underwent a
considerable stylization in the Neolithic period (Figure 2.47). During the
Neolithic, by losing its symbolic meaning and by being enriched by new
elements, the motif of dance and the corresponding friezes were reduced to
sheer decorativeness. All types of ornaments underwent this process (Figure
2.48).

Figure 2.46
|
Examples of friezes with the symmetry group m1 in the late
Paleolithic (Magdalenian) and early Neolithic.
|

Figure 2.47
|
The formation and development of friezes with the symmetry group
m1, with the "kolo" motif, in prehistoric art.
|

Figure 2.48
|
Examples of friezes with the symmetry group m1 in Neolithic art:
(a) Hallaf, around 5000-4500 B.C. The initial motif, the stylized head of a
bull is similar to the Egyptian symbol "ankh"; (b) Hallaf; (c) Crete. The
motif of double ax, "labris", was very often used in early Greek ornaments.
|
Owing to a glide reflection and reflections in reflection lines
perpendicular to the frieze axis, friezes with the symmetry group
mg, among geometric ornaments occur as symbols of regular alternating
phenomena (Figure 2.49-2.51). Different variations of these friezes have
in ethnical art the following meanings (Figure 2.54a, b, c, d): "Up and
down", "The daily motion of the Sun", "The Sun above and below the water
level (the horizon)", "Breathing", "Water", "The rhythm of water".
Figure 2.49
|
Examples of friezes with the symmetry group mg in Paleolithic
art.
|
Figure 2.50
|
Examples of friezes with the symmetry group mg in Neolithic art:
(a) the early Neolithic of Europe; (b) Catal Hüjük, around 6400-5800
B.C.; (c) Hallaf, around 6000 B.C. (7600-6900 B.C.?); (d) Hasuna, Iraq; (e)
Magelmose, 7500-6500 B.C.; (f) Pakistan around 3000 B.C.; (g) the
pre-dynastic period of Egypt, around 4200-3600 B.C.
|
Figure 2.51
|
Examples of friezes with the symmetry group mg: (a) Eynan,
Palestine, around 10000 B.C.; (b) Aznabegovo-Vrshnik, Yugoslavia, around
5000 B.C.; (c) Naqda culture, the pre-dynastic period of Egypt; (d) Mycenae.
|
Friezes with the symmetry group mm (Figure 2.52, 2.53)
often symbolize an even flow of time, years and similar phenomena with a
high degree of symmetry (Figure 2.54f, g, h). It is interesting that in such
cases time is considered as non-polar. Owing to the maximal degree of
symmetry and to the fact that it contains all the other discrete symmetry
groups of friezes as subgroups, besides having a significant independent
function, the symmetry group mm will be a basis from which all
the other discrete symmetry groups of friezes can be derived by means of the
desymmetrization method. Having in mind the fixed shape of the fundamental
region - rectilinear, perpendicular, unbounded fundamental region - a
variety of friezes with the symmetry group mm can be achieved
only by using different elementary asymmetric figures belonging to the
fundamental region. This holds for all the symmetry groups of friezes
generated by reflections (m1, mm).

Figure 2.52
|
Friezes with the symmetry group mm in Paleolithic art.
|

Figure 2.53
|
Friezes with the symmetry group mm in the Paleolithic
(Magdalenian, around 10000 B.C.) and Neolithic.
|
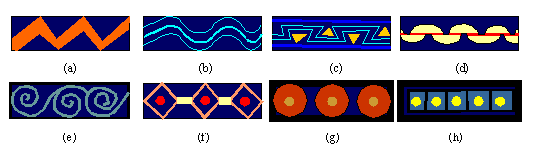
Figure 2.54
|
Examples of friezes in the ethnical art, that possess
precise symbolic meanings and the corresponding names: (a) "Up and down",
"The Sun", Water", "Breathing"; (b) "The rhythm of water" (Congo); (c) The
Sun above and below water (horizon)" (Pueblo Indians); (d) "Days of the full
Moon" (Celebes); (e) Ëndless running of the years" (Celebes); (f), (g), (h)
"The continual motion of the Sun" (Fiji).
|
Already in ornamental art of the Neolithic and of the first great
cultures - the Egyptian, Mesopotamian, and Aegean cultures, and the
pre-Columbian culture in America, etc. - by introducing new ornamental
motifs and by enriching existing ones, the variety of friezes is achieved
(Figure 2.55). Like for rosettes, superpositions of friezes are frequent.
Some primary symbolic meanings have been gradually replaced by new ones.
The application of different motifs unavoidably leads to decorativeness. The
empirical perception of the properties of friezes and the regularities they
are based on, resulted in new friezes constructed by using the construction
rules comprehended, thus opening the way to artistic imagination and
creation-play.
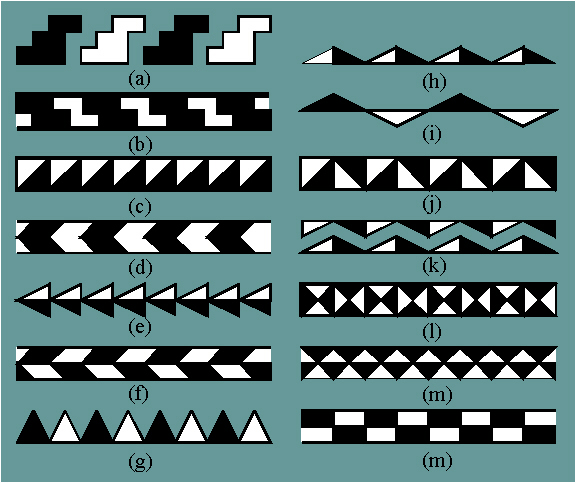
Figure 2.55
|
Antisymmetry friezes in Neolithic ornamental art: (a) 11/
11, Greece, around 3000 B.C.; (b) 12/12, Greece; (c)
12/11, Near East, around 5000 B.C.; (d)
1m/1m, Near East, around 5000 B.C.; (e) 1m/
11, Near East; (f) 1m/11, Anadolia, around 5000 B.C.;
(g) m1/m1, Near East; (h) m1/11,
Near East; (i) mg/11, Greece; (j) mg/
1g, Near East, around 5000 B.C.; (k) mg/12, Anadolia;
(l) mm/mm, Tell el Hallaf, around 4900-4500 B.C.; (m)
mm/m1, Hacilar, about 5500-5200 B.C.; (n)
mm/mg, Near East.
|
*
*
*
Examples of all seven discrete symmetry groups of friezes 11,
1g, 12, m1, 1m, mg,
mm and two continuous visually presentable symmetry groups of
friezes m01 and m0m, represented in bone engravings
or cave drawings, date from Paleolithic art. In ornamental art, friezes
are a way to express regularity, repetition and periodicity, while with
polar friezes, where there occurs a singular oriented direction, they
represent a way to express motion or dynamic tendencies.
In the theory of symmetry, although derived relatively late by
registering the one-dimensional subgroups of the symmetry groups of
ornaments G2 (G. Pòlya, 1924;
P. Niggli, 1924; A. Speiser, 1927), the
symmetry groups of friezes are a suitable ground for different research.
For example, the development of the theory of antisymmetry is greatly
stimulated by studies of the symmetry groups of friezes. Namely, its first
accomplishment - the antisymmetry groups of friezes (H. Heesch, 1929;
H.J. Woods, 1935;
A.V. Shubnikov, 1951) - resulted from the Weber diagrams
of the symmetry groups of bands G321. Owing to their simplicity, the
symmetry groups of friezes G21 - the first category of infinite
isometry groups - were used as a suitable medium for constructing and
analyzing new theories, e.g., the theory of antisymmetry, colored symmetry,
etc.
In the same way as with rosettes, according to the principle of
visual entropy - maximal visual and constructional simplicity and maximal
symmetry - there may be established a relation between geometric
properties of the symmetry groups of friezes and their visual
interpretations - friezes, their frequency of occurrence, period of origin
and variety. The earlier appearance and dominance of friezes satisfying
this principle, is evident.
The table of the group-subgroup relations points to the possibility
to apply the desymmetrization method for the derivation of the symmetry
groups of friezes. According to the relations (Figure 2.56) and the tables
of the (minimal) indexes of subgroups in groups, the classical-symmetry,
antisymmetry (for subgroups of the index 2) and color-symmetry
desymmetrizations or their combinations can be used aiming to obtain the
symmetry groups of friezes of a lower degree of symmetry.
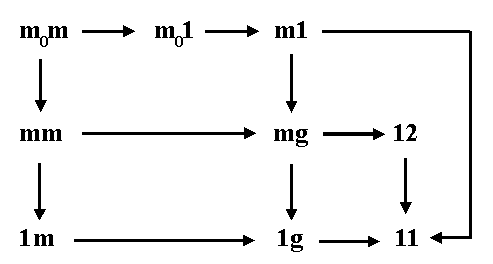
Figure 2.56
A survey of the antisymmetry desymmetrizations of friezes is given
in the corresponding table. Symbols of antisymmetry groups G' are given in
the group/subgroup notation G/H, offering information on the generating
symmetry group G and its subgroup H of the index 2 - symmetry
subgroup H of the group G', which is the final result of the
antisymmetry desymmetrization. So that, by antisymmetry desymmetrizations
it is possible to obtain all subgroups of the index 2 of the given symmetry
group (H.S.M. Coxeter, 1985).
The table of antisymmetry desymmetrizations of symmetry groups of friezes
G21:
|
11 / 11 | m1 / m1 | mg / m1 | mm / mm
|
|
| m1 / 11 | mg / 12 | mm / mg
|
|
1g / 11 | | mg / 1g | mm / 1m
|
|
| 1m / 1m | | mm / m1
|
|
12 / 12 | 1m / 1g | | mm / 12
|
|
12 / 11 | 1m / 11 | |
|
|
The table of the color-symmetry desymmetrizations relies on the
works of J.D. Jarratt, R.L.E. Schwarzenberger (1980)
and H.S.M. Coxeter (1987). By color-symmetry desymmetrizations, the symmetry groups of friezes
11, 1g, 1m, m1 and
12, may be obtained. Complete information on the color-symmetry
desymmetrizations of friezes is given in the corresponding table. Each of
the infinite classes of colored symmetry groups is denoted by a symbol
G/H/H1; its first datum represents the generating symmetry group G, the
second its stationary subgroup H consisting of transformations of the
colored symmetry group G* that maintain each individual index
(color) unchanged, and the third the symmetry subgroup H1 of the group
G* . The symmetry group H1 is the final result of the
color-symmetry desymmetrization. A number N (N ³ 3) is the number of
"colors" used to obtain the particular color-symmetry group. For H = H1,
i.e. iff H is a normal subgroup of the group G, the symbol G/H/H1 is
reduced to the symbol G/H.
The table of color-symmetry desymmetrizations of symmetry groups of friezes
G21:
|
| N | 11/11
|
|
| |
|
|
| N = 0 (mod 2) | 1g/11
|
|
| N = 1 (mod 2) | 1g/1g
|
|
| |
|
|
| N | m1/m1/11
|
|
| N = 0 (mod 2) | m1/11
|
|
| |
|
|
| N | 12/12/11
|
|
| N = 0 (mod 2) | 12/11
|
|
| |
|
|
| N | 1m/1m
|
|
| N = 0 (mod 2) | 1m/1g
|
|
| N = 0 (mod 2) | 1m/11
|
|
| |
|
|
| N = 1 (mod 2) | mg/mg/1g
|
|
| N = 0 (mod 2) | mg/m1/11
|
|
| N = 0 (mod 2) | mg/12/11
|
|
| N = 2 (mod 4) | mg/1g
|
|
| N = 0 (mod 4) | mg/11
|
|
| |
|
|
| N | mm/mm/1m
|
|
| N = 0 (mod 2) (N ³ 6) | mm/m1/11
|
|
|
| N = 0 (mod 2) | mm/mg/1g
|
|
| N = 0 (mod 2) (N ³ 6) | mm/12/11
|
|
| N = 0 (mod 2) | mm/1m
|
|
| N = 0 (mod 4) | mm/11
|
|
| N = 0 (mod 4) | mm/1g
|
|
| N = 4 | mm/m1
|
|
| N = 4 | mm/12
|
|
Due to the objective stationariness of works of ornamental art,
continuous friezes with a polar or bipolar axis do not have adequate visual
interpretations. The visual models of these groups can be constructed by
using textures (A.V. Shubnikov, N.V. Belov et al., 1964).
According to the principle of maximal symmetry, a survey of
group-subgroup relations may, in a way, serve as an indicator of the
frequency of occurrence of the particular symmetry groups of friezes in
ornamental art, and also for recognition and evidence of symmetry
substructures. The influence of the principle of maximal symmetry on the
frequency of occurrence of certain symmetry groups of friezes in ornamental
art comes to its full expression for the most common frieze - the straight
line, which represents a visual illustration of the maximal continuous
symmetry group of friezes m0m and in the frequent occurrence of
friezes with the symmetry groups mm, mg, etc.
The origin of friezes arose also out of the existence of natural
models, so that friezes with the symmetry group 12 or
mg may be considered as stylized forms of waves; motifs with the symmetry
1g or 1m, that are found in arrangements of leaves in
many plants, served as a source of many friezes; while the importance of
mirror symmetry in nature caused friezes with the symmetry group
m1, 1m or mm. This especially refers to the
maximal discrete symmetry group of friezes mm, which contains as
subgroups all the other discrete symmetry groups of friezes and the symmetry
group of rosettes D2 (2m) and expresses, in the
visual sense, the relation "vertical-horizontal" and the quality of
perpendicularity. Besides natural objects, the origin of friezes is also to
be found in the periodic character of many natural phenomena (the turn of
day and night, the turn of the seasons, the phases of the moon, the tides
etc.). Therefore, friezes represent a record of the first human attempts to
register periodic natural phenomena, i.e. the first calendars. In time, with
their symbolic meanings clearly defined, friezes became a visual
communication means: each frieze contains a message, i.e. its meaning is
harmonized with its visual form. This can be proved by the preserved names
of friezes in ethnical art. Later, with the development of all other
communication means, friezes lose their original symbolic function, to be
partially or completely replaced by a decorative one.
The visual impression produced by a real frieze results from the
interaction between its symmetry group, human mirror symmetry and
binocularity, the symmetry group of a limited part of the plane to which the
frieze belongs, and the symmetry group D2 (2m) caused
by the fundamental natural directions - the vertical and horizontal line.
Regarding the first, the other symmetry groups mentioned have a role of
desymmetrization or symmetrization factors. Besides the objective elements
of symmetry, the visual impression is influenced by the subjective elements
referring to the physiological-psychological properties of the visual
perception (e.g., perception of the "right" diagonal as "ascending" and the
"left" as "descending", etc.), so that this dependence may be very complex.
Aiming to perceive and recognize the objective, geometric symmetry, the
observer must eliminate these secondary, subjective visual factors.
A fundamental region of the symmetry group of friezes m1
or mm is rectilinear, with boundaries incident withthe reflection
lines. All the other friezes with partly or completely curved boundaries of
the fundamental region, offer a change of its shape. Aiming to increase the
variety of friezes with the symmetry group m1 or mm
possessing a rectilinear fundamental region, these possibilities are reduced
to the use of different elementary asymmetric figures belonging to the
fundamental region.
Data on the polarity of friezes and enantiomorphism, in the visual
sense refer to the dynamic or static impression created by them. Friezes
with the symmetry groups 11, 1g, 1m with a
polar, oriented singular direction will produce a dynamic effect. Since all
friezes with the polar axis may have a curvilinear fundamental region,
their visual dynamism may be emphasized by choosing an acuteangular
fundamental region with the acute angle oriented toward the direction of
the axis or by choosing an acuteangular elementary asymmetric figure
belonging to the fundamental region and directed in the same way. The
symmetry group of friezes 12 that contains a central reflection
and possesses the bipolar axis, offers a similar possibility: recognition of
two oppositely oriented polar friezes with the symmetry group 11,
which produce the visual impression of two-way motion.
Since the discrete symmetry groups m1, mg and
mm and the continuous groups m01 and m0m
contain reflections with reflection lines perpendicular to the frieze axis,
friezes corresponding to them belong to a family of friezes with
a non-polar axis. Enantiomorphic modifications of friezes with
the discrete symmetry groups 1g, m1, 1m,
mg and mm and continuous visually presentable symmetry
groups m01 and mm, which contain indirect
isometries - reflections or glide reflections - does not
occur.
Data on the polarity of friezes and enantiomorphism may be a basic
indicator of the static or dynamic visual properties of friezes. Non-polar
friezes produce static, while polar friezes produce a dynamic visual
impression. Another component of a dynamic visual impression produced by a
certain frieze, may be the presence of a glide reflection, suggesting the
impression of alternating motion. The enantiomorphism is the "left" or
"right" orientation of a frieze - the existence of only "left" or
"right " homologous asymmetric elementary figures or fundamental regions.
According to the principle of maximal symmetry, those symmetry groups of
friezes with a high degree of symmetry, mg and mm,
prevail. Among them, more frequent are static friezes with the symmetry
group mm. Their distinctive stationariness results from the fact
that each of them may be placed in such a position that the reflection lines
corresponding to the rosettal subgroup D2 (2m)
coincide with the fundamental natural directions - the vertical and
horizontal line. For the maximal continuous symmetry group of friezes
m0m that may be visually modeled by a straight (horizontal)
line, a similar argument hold.
A table survey of subgroups of the symmetry groups of friezes and
their decompositions (reducibility) offers complete evidence of their
symmetry substructures. Through its use, a visual recognition of friezes and
rosettes that a particular frieze contains, will be simplified. Certainly,
static substructures with a higher degree of symmetry may be easily
perceived and visually recognized, but low-symmetry substructures demand its
use. Besides the visual simplicity of substructures, possibilities for their
visual recognition will be caused by all the other elements taking part in
the formation of a visual impression: the visual qualities of
suprastructure, visual simplicity, stationariness or dynamism, the relation
of substructures to vertical and horizontal line, to the surrounding, to the
observer, etc.
Cayley diagrams of the symmetry groups of friezes are another
suitable visual interpretation. Besides pointing out characteristics of
generators, relations that consist of the presentation of the
corresponding symmetry group and its structure, they indicate the visual
qualities of the corresponding friezes. In the tables of the graphic
symbols of symmetry elements, similar such information may be given.
The symmetry groups of friezes G21 are the simplest category of
the infinite groups of isometries. In the development of the generalizations
of the theory of symmetry - antisymmetry and colored symmetry, they had a
significant role. Since visual models are the most obvious interpretation of
abstract geometric-algebraic structures, among infinite discrete symmetry
groups, friezes are the simplest and most suitable medium for analyzing
such generalizations.
Through knowledge of the geometric-algebraic properties of the
symmetry groups of friezes, the visual qualities of the corresponding
friezes may be anticipated directly from the presentations and structures
of their symmetry groups. This opens a large field for ornamental design;
for the planning of visual effects produced by friezes; and for aesthetic
analyses based on exact grounds. The presence of generators of infinite
order in the symmetry groups of friezes and their possible
identification with time, results in the occurrence of the time
component, representing for ornamental art the possibility to
suggest motion.