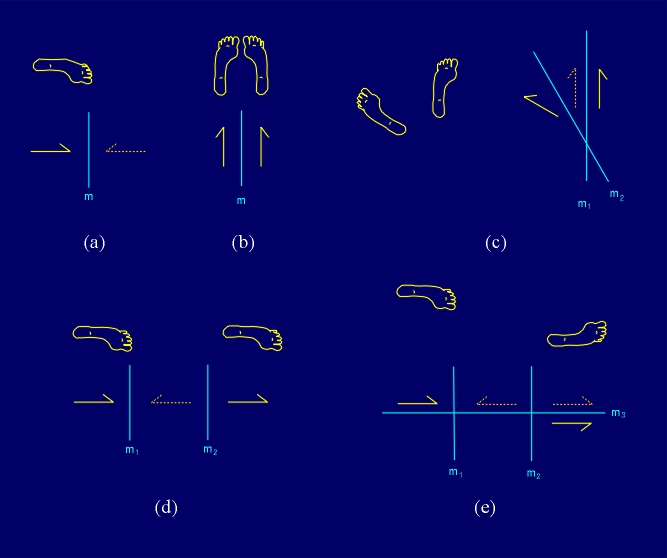
A transformation S of n-dimensional space is called
indirect (or reflective, sense reversing, opposite, odd)
if it transforms any oriented (n+1)-point system onto an
oppositely oriented (n+1)-point system (line segment AB onto
BA, triangle ABC onto ACB, tetrahedron ABCD onto ACBD
in cases of n = 1,2,3 respectively). Otherwise, it is called
direct (sense preserving, even) (Figure 1.6).
(a) Direct and (b) indirect plane isometry.
As an elementary isometric transformation we can take
the reflection, non-identical isometry of space En
(Sn) for which, every point of its subspace En-1
(Sn-1) is an invariant point. In particular, for n = 1 we
have point reflection, for n = 2 line reflection (or
simply - reflection), for n = 3 plane reflection,
involutional indirect isometries. According to the fundamental
theorem on minimal or canonic representation of an
isometric transformation of space En (Sn), which states
that every isometry of this space can be presented as a
composition of maximum n+1 (plane) reflections, it is possible
to classify the isometries of different spaces.
The classification of isometric transformations and
corresponding symmetry groups is common for spaces En, Sn,
Ln for n < 2, while for n ³ 2 different possibilities of
relations of disjoint lines, which are defined by the axiom of
parallelism, condition specific differences. This work
exclusively discusses Euclidean spaces.
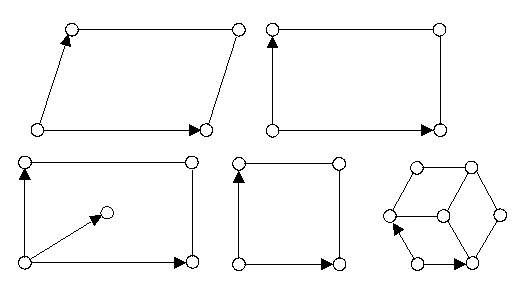
In the space E2 (plane) we distinguish the following
isometric transformations (Figure 1.7):
(a) Identity transformation; (b) reflection; (c) rotation; (d)
translation; (e) glide reflection.
1) identity transformation E, with the minimal reflectional representation
of the length 2 (R2 = E);
2) reflection R;
3) rotation S = R1R2, the product of two reflections in
the reflection lines crossing in the invariant point (center of
rotation). The oriented angle of rotation is equal to twice the
angle between the reflection lines R1, R2;
4) translation X = R1R2, the product of two reflections
with parallel reflection lines, such that the translation vector
is perpendicular to them and equal to twice the oriented distance
between the reflection lines R1, R2;
5) glide reflection P =
R3X = XR3 = R1R2R3, the
commutative product of a translation X and a reflection R3
with the reflection line parallel to the translation axis.
With respect to the invariant figures, all the points of
the plane E2 are invariant points of the identity
transformation E, reflection R maintains the invariance of
all the points of the reflection line, rotation S possesses a
single invariant point - the center of rotation, while
translation and glide reflection have no invariant points. A
glide reflection possesses a single invariant line - the axis,
and a translation keeps invariant all the lines parallel to the
translation axis.
In the case of rotation, if the relation
S = R1R2 =
R2R1 holds, i.e.
if the reflection lines R1,
R2 are perpendicular, as a result we get the special
involutional rotation - central reflection Z (two-fold
rotation, half-turn, point-reflection) (Figure 1.8).
Central reflection Z.
When orientation is considered we distinguish
direct transformations (or sense preserving transformations):
identity transformation E, translation, rotation, and
indirect transformations (sense reversing transformations):
reflection and glide reflection. Since direct transformations are
the product of an even, and the indirect ones of an odd number of
reflections, we can call them respectively even and
odd transformations.
If a symmetry transformation S can be represented as a
composition S = S1¼Sn such that SiSj
= SjSi,
i,j = 1,¼,n, we can call it a complex or
composite transformation while the transformations
S1,¼,Sn we call the dependent
transformations or dependent
elements of symmetry. We will use such approach whenever we
are interested to learn to what degree the dependent elements of
symmetry influence the characteristics of the composite
transformation, and whether they have lost or preserved their
geometric and visual characteristics during it. For example, a
glide reflection is such commutative composition of translation
and reflection, with reflection line parallel to the translation
axis.
An analogous procedure makes possible the classification
of isometries of the space E3, where each isometry can be
represented as the composition of four plane reflections at the
most. Besides the transformations of the space E2 afore
mentioned with the line reflections substituted by plane
reflections, as the new transformations of the space E3 we
have two more transformations. They are a direct isometry -
twist (screw), the commutative composition of a rotation
and a translation, the canonic representation of which consists
of four plane reflections and indirect isometry -
rotatory reflection, the commutative composition of a rotation
and a plane reflection in the plane perpendicular to the rotation
axis, the canonic representation of which consists of three
plane reflections. In particular, the involutional rotatory
reflection, which is the composition of three plane reflections
of which every two commute, is called point inversion Z
(or rotatory inversion).
For every element S1 of a transformation group G we
can define the conjugate of the element S1 by an
element S as the product S-1S1S, which we denote by
S1S. If S1S Î G, then the mapping S1 onto S1S
represents an automorphism of the group G. If the element S
by means of which this automorphism is being realized belongs to
the group G, such an automorphism is called an internal
automorphism. Any other automorphism of a group G is called
an external automorphism. An important characteristic of
a conjugate is that the order of the conjugate S1S is equal
to the order of the element S1. If a figure f is invariant
under a transformation S1, then S(f) is the figure invariant
under transformation S1S. The conjugate of a reflection R
with invariant reflection line p, derived by isometry S, is
the reflection RS with the invariant reflection line S(p).
Hence we can conclude that the isometry S1 and all its
conjugates S1S derived by different isometries S constitute
one class of equivalence, i.e. the class of isometries
having the same name, which means that (internal) automorphism of
a group of isometries G transforms reflections onto
reflections, rotations onto rotations, etc. The properties of
the (internal) automorphisms are frequently used when proving
theorems on isometric transformations and the other symmetry
transformations. For example, by gR, g Î G, is defined an
internal automorphism of the symmetry group of square G, given
by presentation
{S,R} S4 = R2 = (RS)2 = E:
ER = E, RR = R,
(RS)R = SR,
In the same way,
it is defined an external automorphism of the rotational group of
square H, given by presentation
{S} S4 = E,
SR = S3,
(S2)R = S2,
(S3)R = S,
where the
reflection line of reflection R contains the center of
four-fold rotation S. Hence, external automorphisms are very
efficient tool for extending symmetry groups.
Since the product of direct transformations is a direct
transformation, and the inverse of a direct transformation is a
direct transformation, each group of transformations G, which
contains at least one indirect transformation has a subgroup of
the index 2, denoted by G+, which consists of direct
transformations of the group G. For example, the rotational
subgroup of sqare H satisfies this condition regarding the
symmetry group of square, so H = G+, [G:H] = 2. All direct
isometries of the space En can be identified as movements of a
material object in the space En, as opposed to indirect
isometries which do not have such a physical interpretation
(e.g., a plane reflection does not represent motion in E3).
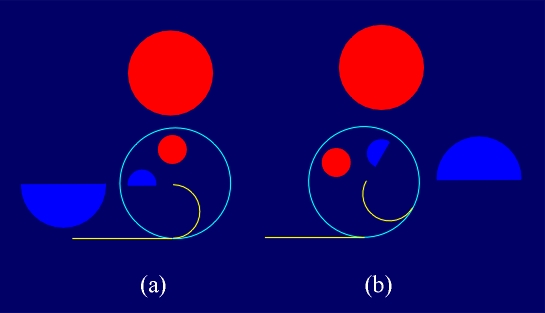
For a figure f with the symmetry group Gf, which
consists only of direct symmetries, it is possible to have the
enantiomorphism - enantiomorphic modifications of
a figure f, i.e. to have the "left" and "right" form of the
figure f (Figure 1.9). The existence of indirect symmetries of
a figure f implies the absence of enantiomorphism.
Since reflections have a role of elementary isometric
transformations, while all other isometries are their finite
compositions, of special interest will be symmetry groups
generated by reflections - groups, a set of generators of
which consists exclusively of reflections. Since every reflection
keeps invariant each point of the reflection line, the
fundamental region of these groups will possess a fixed shape,
will not allow variations and will have rectilinear edges. All
symmetry groups will be subgroups of groups generated by
reflections. In the case of conformal symmetry groups, along with
reflections, circle inversions have the analogous function. For
example, the symmetry group of square is the group generated by
reflections, with the fundamental region of the fixed shape
(Figure 1.3a).
"Left" and "right" rosette with the symmetry group C4,
consisting of direct symmetries.
The results of composition of plane isometries are
different categories of groups of isometries of the space
E2, represented by Bohm symbols as: G210 - symmetry
groups of finite friezes, G20 - symmetry groups of
rosettes, G21 - symmetry groups of friezes
and G2 - symmetry groups of ornaments. Because of the
relation G210 Ì G20, in this work we will discuss
only the categories G20, G21, G2, while the category
G210 will be discussed within the category G20. The
definitions of symmetry groups will be derived directly
from Bohm symbols: symmetry groups of rosettes are groups of
isometries of the space E2 (plane) with an invariant
0-dimensional subspace (point), symmetry groups of friezes are
groups of isometries of the space E2 with an invariant
1-dimensional subspace (line) and without invariant points, while
symmetry groups of ornaments are groups of isometries of the
space E2 without invariant subspaces (points, lines). The
groups of the category Gn are called the space groups,
the groups of the category Gn1 the line groups, and
the groups of the category Gn0 the point groups of
the space En. With symmetry groups of friezes G21 and
symmetry groups of ornaments G2, a group contains one or two
generating translations respectively, so that each of these
groups has a translational subgroup. A lattice is
the orbit of a point with respect to a discrete group of
translations. For the friezes it is a linear series of
equidistant points while for ornaments we get a plane
lattice or simply a lattice. Five different symmetry types of
plane lattices bear the name of Bravais lattices; the
points of these lattices are defined by five different isohedral
tessellations, which consist of parallelograms, rhombuses,
rectangles, squares or regular hexagons. To Bravais lattices
correspond the crystal systems of the same names (Figure
1.10).
Five plane Bravais lattices.
Because the symmetry groups of friezes G21 are
groups of isometries of the plane E2 with an invariant line,
they cannot have rotations of an order greater than 2.
For the symmetry groups of ornaments G2 so-called
crystallographic restriction holds, according to which
symmetry groups of ornaments can have only rotations of the order
n=1,2,3,4,6. The term "crystallographic groups" is
used for all groups which satisfy this condition, despite the
category they belong to.
In isometry groups all distances between points under the
effect of symmetries remain unchanged and the congruence
of homologous figures is preserved. Consequently, the same holds
for all other geometric properties of such figures, so that the
equiangularity (the congruence of the angles of
homologous figures) and their equiformity (the same form of
homologous figures) are the direct consequences of isometrism.
The next class of symmetry groups we shall consider are
the similarity symmetry groups. A similarity
transformation of the space En is a transformation which to
each line segment of length AB assigns a line segment of the
length kAB whereby k is a real positive number, the
coefficient of similarity. In particular, if k = 1 then a
similarity transformation is an isometry. According to the
theorem on the existence of an invariant point of every
similarity transformation which is not an isometry, there are,
besides isometries, three types of similarity symmetry
transformations of the space E2:
(i) central dilatation K (or simply dilatation), a
transformation which to each vector (A,B)
assigns the vector (A',B'), such that
A' = K(A), B' = K(B)
and (A',B') = k(A,B),
where the coefficient of the dilatation is
k Î Â\{-1,0,1} ;
(ii) dilative rotation L, the commutative composition of
a central dilatation K and a rotation, with a common invariant
point;
(iii) dilative reflection M, the commutative
composition of a dilatation K and a reflection in the
reflection line containing the invariant point (center) of the
dilatation K (Figure 1.11).
(a) Dilatation; (b) dilative rotation; (c) dilative reflection.
Those transformations are, in the given order, isomorphic
with the isometries of the space E3: translation, twist and
glide reflection. They make possible the extension of the
symmetry groups of rosettes G20 by the external
automorphism, having as the result similarity symmetry
groups S20 that we will, thanks to the existence of the
invariant point, call the similarity symmetry groups of
rosettes.
Dilatations K and dilative rotations L are direct,
while dilative reflections M are indirect transformations. They
all possess the properties of equiangularity and equiformity. All
other aspects of similarity symmetry groups (the problems of
enantiomorphism, fundamental regions, tessellations,¼)
will be discussed analogously to the case of isometry groups.
Further generalization leads to conformal
transformations or circle preserving transformations of the
plane E2\{O} ; for them the property of
equiangularity has been preserved, but not that of equiformity.
We have, as the elementary transformation of conformal symmetry
in E2\{O} , the circle inversion
RI
(or simply inversion) - an involutional transformation
isomorphic with a reflection, that gives to each point A in
the plane E2\{O} a point A1 so that
(O,A)°(O,A1) = r2, where
r is the radius of the inversion circle c(O,r) and
O is the singular point of the plane E2\{O}
(Figure 1.12). Just like a reflection, for which each point of
the reflection line is invariant, an inversion maintains
invariant each point of the inversion circle. By discussing a
line as a circle with an infinite radius (and treating as
circles, at the same time and under the same term, circles and
lines) it is possible to identify reflections with circle
inversions. In such a case, all circle inversions (including line
reflections) and their compositions, can be discussed as
circle preserving transformations, i.e. transformations mapping
circles (including lines) onto circles.
Circle inversion.
Besides the circle inversion RI, by composing it with
isometries maintaining invariant the circle line c of the
inversion circle c(O,r) - with a reflection with reflection
line containing the circle center O or with a rotation with the
rotation center O, we have two more conformal transformations:
(i) inversional reflection ZI = RIR
= RRI, the
involutional transformation, the commutative composition of a
reflection and a circle inversion;
(ii) inversional
rotation SI = SRI = RIS,
the commutative composition of a
rotation and a circle inversion (Figure 1.13).
(a) Inversional reflection; (b) inversional rotation.
Those three conformal symmetry transformations, besides
isometries and similarity symmetry transformations, constitute
the finite and infinite conformal symmetry groups C21,
C2 - conformal symmetry groups of rosettes in
E2\{O} .
As an extension of the symmetry groups of rosettes
G20 we have the finite conformal symmetry groups
C21 isomorphic with the symmetry groups of tablets
G320. As a further extension of finite conformal symmetry
groups C21 by the similarity symmetry transformations K,
L, M, we get the infinite conformal symmetry groups
C2. The similarity symmetry groups S20 and the infinite
conformal symmetry groups C2 are isomorphic with the line
symmetry groups of the space E3 - the symmetry groups of
rods G31. In line with the isomorphism mentioned, all
similarity symmetry and conformal symmetry transformations offer
a reflectional (canonic) representation by, at most, four
reflections (reflections and circle inversions). By applying this
isomorphism, ornamental motifs which correspond to the similarity
symmetry and conformal symmetry groups, satisfy one more scope of
painting: adequate interpretation of space objects in the plane.
The plane structures obtained are called generalized
projections of the symmetry groups of tablets G320 and rods
G31.


(SR)R = RS,
SR = S3, (S2)R =
S2, (S3)R = S.



NEXT
CONTENTS
