[1]    Ahlfors, L. V. (1978). Complex analysis, Third ed. McGraw-Hill Book Co., New York. An introduction to the theory of analytic functions of one complex variable, International Series in Pure and Applied Mathematics. MR510197 (80c:30001)

[2]    Ahlfors, L. V. (2010). Conformal invariants. AMS Chelsea Publishing, Providence, RI. Topics in geometric function theory, Reprint of the 1973 original, With a foreword by Peter Duren, F. W. Gehring and Brad Osgood. MR2730573

[3]    Aizenman, M. (1997). On the number of incipient spanning clusters. Nuclear Phys. B 485, 3, 551–582. http://dx.doi.org/10.1016/S0550-3213(96)00626-8. MR1431856 (98j:82030)

[4]    Aizenman, M. (1998). Scaling limit for the incipient spanning clusters. In Mathematics of multiscale materials (Minneapolis, MN, 1995–1996). IMA Vol. Math. Appl., Vol. 99. Springer, New York, 1–24. MR1635999 (99g:82034)

[5]    Aizenman, M. and Burchard, A. (1999). Hölder regularity and dimension bounds for random curves. Duke Math. J. 99, 3, 419–453. http://dx.doi.org/10.1215/S0012-7094-99-09914-3. MR1712629 (2000i:60012)

[6]    Aizenman, M., Duplantier, B., and Aharony, A. (1999). Path-crossing exponents and the external perimeter in 2D percolation. Phys. Rev. Lett. 83, 7 (Aug), 1359–1362.

[7]     Aizenman, M., Kesten, H., and Newman, C. M. (1987). Uniqueness of the infinite cluster and continuity of connectivity functions for short and long range percolation. Comm. Math. Phys. 111, 4, 505–531. http://projecteuclid.org/getRecord?id=euclid.cmp/1104159720.
MR901151 (89b:82060)

[8]    Alon, N., Benjamini, I., and Stacey, A. (2004). Percolation on finite graphs and isoperimetric inequalities. Ann. Probab. 32, 3A, 1727–1745. http://dx.doi.org/10.1214/009117904000000414. MR2073175 (2005f:05149)

[9]    Beffara, V. (2004). Hausdorff dimensions for SLE₆. Ann. Probab. 32, 3B, 2606–2629. http://dx.doi.org/10.1214/009117904000000072. MR2078552 (2005k:60295)

[10]    Beffara, V. (2007). Cardy’s formula on the triangular lattice, the easy way. In Universality and renormalization. Fields Inst. Commun., Vol. 50. Amer. Math. Soc., Providence, RI, 39–45. MR2310300 (2008i:82030)

[11]    Beffara, V. (2008a). The dimension of the SLE curves. Ann. Probab. 36, 4, 1421–1452. http://dx.doi.org/10.1214/07-AOP364.
MR2435854 (2009e:60026)

[12]    Beffara, V. (2008b). Is critical 2D percolation universal? In In and out of equilibrium. 2. Progr. Probab., Vol. 60. Birkhäuser, Basel, 31–58. http://dx.doi.org/10.1007/978-3-7643-8786-0_3. MR2477376 (2010h:60262)

[13]    Beffara, V. and Duminil-Copin, H. (2011). Planar percolation with a glimpse of Schramm-Loewner evolution. ArXiv preprint.

[14]    Benjamini, I. and Kozma, G. (2011). ℤ-actions and uniqueness of percolation. ArXiv preprint.

[15]    Benjamini, I., Lyons, R., Peres, Y., and Schramm, O. (1999a). Critical percolation on any nonamenable group has no infinite clusters. Ann. Probab. 27, 3, 1347–1356. http://dx.doi.org/10.1214/aop/1022677450. MR1733151 (2000k:60197)

[16]    Benjamini, I., Lyons, R., Peres, Y., and Schramm, O. (1999b). Group-invariant percolation on graphs. Geom. Funct. Anal. 9, 1, 29–66. http://dx.doi.org/10.1007/s000390050080. MR1675890 (99m:60149)

[17]    Benjamini, I. and Schramm, O. (1998). Conformal invariance of Voronoi percolation. Comm. Math. Phys. 197, 1, 75–107. http://dx.doi.org/10.1007/s002200050443. MR1646475 (99i:60172)

[18]    Billingsley, P. (1999). Convergence of probability measures, Second ed. Wiley Series in Probability and Statistics: Probability and Statistics. John Wiley & Sons Inc., New York. A Wiley-Interscience Publication, http://dx.doi.org/10.1002/9780470316962. MR1700749 (2000e:60008)

[19]    Binder, I., Chayes, L., and Lei, H. K. (2010a). On convergence to SLE₆ I: conformal invariance for certain models of the bond-triangular type. J. Stat. Phys. 141, 2, 359–390. http://dx.doi.org/10.1007/s10955-010-0052-3. MR2726646

[20]    Binder, I., Chayes, L., and Lei, H. K. (2010b). On convergence to SLE₆ II: discrete approximations and extraction of Cardy’s formula for general domains. J. Stat. Phys. 141, 2, 391–408. http://dx.doi.org/10.1007/s10955-010-0053-2. MR2726647

[21]    Bollobás, B. (2001). Random graphs, Second ed. Cambridge Studies in Advanced Mathematics, Vol. 73. Cambridge University Press, Cambridge. MR1864966 (2002j:05132)

[22]    Bollobás, B. and Kohayakawa, Y. (1994). Percolation in high dimensions. European J. Combin. 15, 2, 113–125. http://dx.doi.org/10.1006/eujc.1994.1014. MR1261058 (95c:60092)

[23]    Bollobás, B. and Riordan, O. (2006). Percolation. Cambridge University Press, New York. MR2283880 (2008c:82037)

[24]    Borgs, C., Chayes, J. T., Kesten, H., and Spencer, J. (2001). The birth of the infinite cluster: finite-size scaling in percolation. Comm. Math. Phys. 224, 1, 153–204. Dedicated to Joel L. Lebowitz, http://dx.doi.org/10.1007/s002200100521. MR1868996 (2002k:60199)

[25]    Borgs, C., Chayes, J. T., van der Hofstad, R., Slade, G., and Spencer, J. (2005a). Random subgraphs of finite graphs. I. The scaling window under the triangle condition. Random Structures Algorithms 27, 2, 137–184. http://dx.doi.org/10.1002/rsa.20051. MR2155704 (2006e:05156)

[26]    Borgs, C., Chayes, J. T., van der Hofstad, R., Slade, G., and Spencer, J. (2005b). Random subgraphs of finite graphs. II. The lace expansion and the triangle condition. Ann. Probab. 33, 5, 1886–1944. http://dx.doi.org/10.1214/009117905000000260. MR2165583 (2006j:60009)

[27]    Borgs, C., Chayes, J. T., van der Hofstad, R., Slade, G., and Spencer, J. (2006). Random subgraphs of finite graphs. III. The phase transition for the n-cube. Combinatorica 26, 4, 395–410. http://dx.doi.org/10.1007/s00493-006-0022-1. MR2260845 (2007k:05194)

[28]    Broadbent, S. R. and Hammersley, J. M. (1957). Percolation processes. I. Crystals and mazes. Proc. Cambridge Philos. Soc. 53, 629–641. MR0091567 (19,989e)

[29]    Burton, R. M. and Keane, M. (1989). Density and uniqueness in percolation. Comm. Math. Phys. 121, 3, 501–505. http://projecteuclid.org/getRecord?id=euclid.cmp/1104178143. MR990777 (90g:60090)

[30]    Camia, F. and Newman, C. M. (2006). Two-dimensional critical percolation: the full scaling limit. Comm. Math. Phys. 268, 1, 1–38. http://dx.doi.org/10.1007/s00220-006-0086-1. MR2249794 (2007m:82032)

[31]    Camia, F. and Newman, C. M. (2007). Critical percolation exploration path and SLE₆: a proof of convergence. Probab. Theory Related Fields 139, 3-4, 473–519. http://dx.doi.org/10.1007/s00440-006-0049-7. MR2322705 (2008k:82040)

[32]    Carathéodory, C. (1913). Über die Begrenzung einfach zusammenhängender Gebiete. Math. Ann. 73, 3, 323–370.  http://dx.doi.org/10.1007/BF01456699. MR1511737

[33]    Cardy, J. (2001). Conformal invariance and percolation. ArXiv preprint.

[34]    Cardy, J. L. (1992). Critical percolation in finite geometries. J. Phys. A 25, 4, L201–L206. http://stacks.iop.org/0305-4470/25/L201. MR1151081 (92m:82048)

[35]    Chayes, L. and Lei, H. K. (2007). Cardy’s formula for certain models of the bond-triangular type. Rev. Math. Phys. 19, 5, 511–565. http://dx.doi.org/10.1142/S0129055X0700305X. MR2337476 (2008j:82019)

[36]    Chelkak, D. and Smirnov, S. (2009). Universality in the 2D Ising model and conformal invariance of fermionic observables. ArXiv preprint.

[37]    Chelkak, D. and Smirnov, S. (2010). Conformal invariance of the 2D Ising model at criticality. In preparation.

[38]    Ding, J., Kim, J. H., Lubetzky, E., and Peres, Y. (2011). Anatomy of a young giant component in the random graph. Random Structures Algorithms 39, 2, 139–178. http://dx.doi.org/10.1002/rsa.20342.

[39]    Dubédat, J. (2005). SLE(κ,ρ) martingales and duality. Ann. Probab. 33, 1, 223–243. http://dx.doi.org/10.1214/009117904000000793. MR2118865 (2005j:60180)

[40]    Dubédat, J. (2006). Excursion decompositions for SLE and Watts’ crossing formula. Probab. Theory Related Fields 134, 3, 453–488. http://dx.doi.org/10.1007/s00440-005-0446-3. MR2226888 (2007d:60019)

[41]    Dubédat, J. (2009). Duality of Schramm-Loewner evolutions. Ann. Sci. Éc. Norm. Supér. (4) 42, 5, 697–724. MR2571956 (2011g:60151)

[42]    Dudley, R. M. (1968). Distances of probability measures and random variables. Ann. Math. Statist 39, 1563–1572. MR0230338 (37 #5900)

[43]    Duminil-Copin, H. and Smirnov, S. (2010). The connective constant of the honeycomb lattice equals 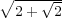. ArXiv preprint.

[44]    Duminil-Copin, H. and Smirnov, S. (2011). Conformal invariance of lattice models. ArXiv preprint.

[45]    Epstein, D. B. A. (1981). Prime ends. Proc. London Math. Soc. (3) 42, 3, 385–414. http://dx.doi.org/10.1112/plms/s3-42.3.385. MR614728 (83c:30025)

[46]    Fortuin, C. M., Kasteleyn, P. W., and Ginibre, J. (1971). Correlation inequalities on some partially ordered sets. Comm. Math. Phys. 22, 89–103. MR0309498 (46 #8607)

[47]    Grimmett, G. (1999). Percolation, Second ed. Grundlehren der Mathematischen Wissenschaften, Vol. 321. Springer-Verlag, Berlin. MR1707339 (2001a:60114)

[48]    Grimmett, G. (2010). Probability on graphs. Institute of Mathematical Statistics Textbooks, Vol. 1. Cambridge University Press, Cambridge. Random processes on graphs and lattices. MR2723356

[49]    Grimmett, G. R. and Stacey, A. M. (1998). Critical probabilities for site and bond percolation models. Ann. Probab. 26, 4, 1788–1812. http://dx.doi.org/10.1214/aop/1022855883. MR1675079 (2000d:60160)

[50]    Hara, T. and Slade, G. (1990). Mean-field critical behaviour for percolation in high dimensions. Comm. Math. Phys. 128, 2, 333–391. http://projecteuclid.org/getRecord?id=euclid.cmp/1104180434. MR1043524 (91a:82037)

[51]    Hara, T. and Slade, G. (1994). Mean-field behaviour and the lace expansion. In Probability and phase transition (Cambridge, 1993). NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci., Vol. 420. Kluwer Acad. Publ., Dordrecht, 87–122. MR1283177 (95d:82033)

[52]    Hara, T. and Slade, G. (1995). The self-avoiding-walk and percolation critical points in high dimensions. Combin. Probab. Comput. 4, 3, 197–215. http://dx.doi.org/10.1017/S0963548300001607. MR1356575 (96i:82081)

[53]    Harris, T. E. (1960). A lower bound for the critical probability in a certain percolation process. Proc. Cambridge Philos. Soc. 56, 13–20. MR0115221 (22 #6023)

[54]    Hongler, C. and Smirnov, S. (2010). The energy density in the planar Ising model. ArXiv preprint.

[55]    Ikhlef, Y. and Rajabpour, M. A. (2011). Discrete holomorphic parafermions in the Ashkin-Teller model and SLE. J. Phys. A 44, 4, 042001, 11. http://dx.doi.org/10.1088/1751-8113/44/4/042001. MR2754707

[56]    Kager, W. and Nienhuis, B. (2004). A guide to stochastic Löwner evolution and its applications. J. Statist. Phys. 115, 5-6, 1149–1229. http://dx.doi.org/10.1023/B:JOSS.0000028058.87266.be. MR2065722 (2005f:82037)

[57]    Kakutani, S. (1944). Two-dimensional Brownian motion and harmonic functions. Proc. Imp. Acad. Tokyo 20, 706–714. MR0014647 (7,315b)

[58]    Karatzas, I. and Shreve, S. E. (1991). Brownian motion and stochastic calculus, Second ed. Graduate Texts in Mathematics, Vol. 113. Springer-Verlag, New York. MR1121940 (92h:60127)

[59]    Kemppainen, A. and Smirnov, S. (2011). Conformal invariance in random cluster models. III. Full scaling limit. In preparation.

[60]    Kenyon, R. (2000). Conformal invariance of domino tiling. Ann. Probab. 28, 2, 759–795. http://dx.doi.org/10.1214/aop/1019160260.
MR1782431 (2002e:52022)

[61]    Kenyon, R. (2001). Dominos and the Gaussian free field. Ann. Probab. 29, 3, 1128–1137. http://dx.doi.org/10.1214/aop/1015345599.
MR1872739 (2002k:82039)

[62]    Kenyon, R. (2011). Conformal invariance of loops in the double-dimer model. ArXiv preprint.

[63]    Kenyon, R. W. and Wilson, D. B. (2011). Boundary partitions in trees and dimers. Trans. Amer. Math. Soc. 363, 3, 1325–1364. http://dx.doi.org/10.1090/S0002-9947-2010-04964-5. MR2737268 (2011i:60023)

[64]    Kesten, H. (1980). The critical probability of bond percolation on the square lattice equals 1 2. Comm. Math. Phys. 74, 1, 41–59. http://projecteuclid.org/getRecord?id=euclid.cmp/1103907931. MR575895 (82c:60179)

[65]    Kesten, H. (1982). Percolation theory for mathematicians. Progress in Probability and Statistics, Vol. 2. Birkhäuser Boston, Mass. MR692943 (84i:60145)

[66]    Kesten, H. (1990). Asymptotics in high dimensions for percolation. In Disorder in physical systems. Oxford Sci. Publ. Oxford Univ. Press, New York, 219–240. MR1064563 (91k:60114)

[67]    Kesten, H., Sidoravicius, V., and Zhang, Y. (1998). Almost all words are seen in critical site percolation on the triangular lattice. Electron. J. Probab. 3, no. 10, 75 pp. (electronic).  http://www.math.washington.edu/∼ejpecp/EjpVol3/paper10.abs.html. MR1637089 (99j:60155)

[68]    Lalley, S., Lawler, G., and Narayanan, H. (2009). Geometric interpretation of half-plane capacity. Electron. Commun. Probab. 14, 566–571. MR2576752 (2011b:60332)

[69]    Langlands, R., Pouliot, P., and Saint-Aubin, Y. (1994). Conformal invariance in two-dimensional percolation. Bull. Amer. Math. Soc. (N.S.) 30, 1, 1–61. http://dx.doi.org/10.1090/S0273-0979-1994-00456-2. MR1230963 (94e:82056)

[70]    Lawler, G. (2009). Schramm-Loewner evolution (SLE). In Statistical mechanics. IAS/Park City Math. Ser., Vol. 16. Amer. Math. Soc., Providence, RI, 231–295. MR2523461 (2011d:60244)

[71]    Lawler, G., Schramm, O., and Werner, W. (2003). Conformal restriction: the chordal case. J. Amer. Math. Soc. 16, 4, 917–955 (electronic). http://dx.doi.org/10.1090/S0894-0347-03-00430-2. MR1992830 (2004g:60130)

[72]    Lawler, G. F. (2005). Conformally invariant processes in the plane. Mathematical Surveys and Monographs, Vol. 114. American Mathematical Society, Providence, RI. MR2129588 (2006i:60003)

[73]    Lawler, G. F., Schramm, O., and Werner, W. (2001a). Values of Brownian intersection exponents. I. Half-plane exponents. Acta Math. 187, 2, 237–273. http://dx.doi.org/10.1007/BF02392618.
MR1879850 (2002m:60159a)

[74]    Lawler, G. F., Schramm, O., and Werner, W. (2001b). Values of Brownian intersection exponents. II. Plane exponents. Acta Math. 187, 2, 275–308. http://dx.doi.org/10.1007/BF02392619.
MR1879851 (2002m:60159b)

[75]    Lawler, G. F., Schramm, O., and Werner, W. (2002a). One-arm exponent for critical 2D percolation. Electron. J. Probab. 7, no. 2, 13 pp. (electronic). http://www.math.washington.edu/∼ejpecp/EjpVol7/paper2.abs.html. MR1887622 (2002k:60204)

[76]    Lawler, G. F., Schramm, O., and Werner, W. (2002b). Values of Brownian intersection exponents. III. Two-sided exponents. Ann. Inst. H. Poincaré Probab. Statist. 38, 1, 109–123. http://dx.doi.org/10.1016/S0246-0203(01)01089-5. MR1899232 (2003d:60163)

[77]     Lawler, G. F., Schramm, O., and Werner, W. (2004). Conformal invariance of planar loop-erased random walks and uniform spanning trees. Ann. Probab. 32, 1B, 939–995. http://dx.doi.org/10.1214/aop/1079021469. MR2044671 (2005f:82043)

[78]    Lawler, G. F. and Sheffield, S. (2009). The natural parametrization for the Schramm-Loewner evolution. ArXiv preprint.

[79]    Lawler, G. F. and Werner, W. (2000). Universality for conformally invariant intersection exponents. J. Eur. Math. Soc. (JEMS) 2, 4, 291–328. http://dx.doi.org/10.1007/s100970000024. MR1796962 (2002g:60123)

[80]    Lévy, P. (1992). Processus stochastiques et mouvement brownien. Les Grands Classiques Gauthier-Villars. Éditions Jacques Gabay, Sceaux. Followed by a note by M. Loève, Reprint of the second (1965) edition. MR1188411 (93i:60003)

[81]    Lieb, E. H. and Loss, M. (2001). Analysis, Second ed. Graduate Studies in Mathematics, Vol. 14. American Mathematical Society, Providence, RI. MR1817225 (2001i:00001)

[82]    Marshall, D. E. and Rohde, S. (2005). The Loewner differential equation and slit mappings. J. Amer. Math. Soc. 18, 4, 763–778 (electronic). http://dx.doi.org/10.1090/S0894-0347-05-00492-3. MR2163382 (2006d:30022)

[83]    Mendelson, D., Nachmias, A., Sheffield, S., and Watson, S. (2011). Convergence rate in Cardy’s formula. In preparation.

[84]    Miller, J. (2010a). Fluctuations for the Ginzburg-Landau ∇ϕ interface model on a bounded domain. ArXiv preprint.

[85]    Miller, J. (2010b). Universality for SLE(4). ArXiv preprint.

[86]    Miller, J. and Sheffield, S. (2011). CLE(4) and the Gaussian free field. In preparation.

[87]    Mörters, P. and Peres, Y. (2010). Brownian motion. Cambridge Series in Statistical and Probabilistic Mathematics. Cambridge University Press, Cambridge. With an appendix by Oded Schramm and Wendelin Werner. MR2604525

[88]    Munkres, J. R. (2000). Topology, Second ed. Prentice Hall, Upper Saddle River, NJ.

[89]    Nachmias, A. (2009). Mean-field conditions for percolation on finite graphs. Geom. Funct. Anal. 19, 4, 1171–1194. http://dx.doi.org/10.1007/s00039-009-0032-4. MR2570320 (2011e:60228)

[90]    Pommerenke, C. (1992). Boundary behaviour of conformal maps. Grundlehren der Mathematischen Wissenschaften, Vol. 299. Springer-Verlag, Berlin. MR1217706 (95b:30008)

[91]    Reimer, D. (2000). Proof of the van den Berg-Kesten conjecture. Combin. Probab. Comput. 9, 1, 27–32. http://dx.doi.org/10.1017/S0963548399004113. MR1751301 (2001g:60017)

[92]    Rohde, S. and Schramm, O. (2005). Basic properties of SLE. Ann. of Math. (2) 161, 2, 883–924. http://dx.doi.org/10.4007/annals.2005.161.883. MR2153402 (2006f:60093)

[93]    Russo, L. (1978). A note on percolation. Z. Wahrscheinlichkeitstheorie und Verw. Gebiete 43, 1, 39–48. MR0488383 (58 #7931)

[94]    Schramm, O. (2000). Scaling limits of loop-erased random walks and uniform spanning trees. Israel J. Math. 118, 221–288. http://dx.doi.org/10.1007/BF02803524. MR1776084 (2001m:60227)

[95]    Schramm, O. (2001). A percolation formula. Electron. Comm. Probab. 6, 115–120 (electronic). MR1871700 (2002h:60227)

[96]    Schramm, O. (2007). Conformally invariant scaling limits: an overview and a collection of problems. In International Congress of Mathematicians. Vol. I. Eur. Math. Soc., Zürich, 513–543. http://dx.doi.org/10.4171/022-1/20. MR2334202 (2008j:60237)

[97]    Schramm, O. and Sheffield, S. (2005). Harmonic explorer and its convergence to SLE₄. Ann. Probab. 33, 6, 2127–2148. http://dx.doi.org/10.1214/009117905000000477. MR2184093 (2006i:60013)

[98]    Schramm, O. and Sheffield, S. (2009). Contour lines of the two-dimensional discrete Gaussian free field. Acta Math. 202, 1, 21–137. http://dx.doi.org/10.1007/s11511-009-0034-y. MR2486487 (2010f:60238)

[99]    Schramm, O. and Sheffield, S. (2010). A contour line of the continuum Gaussian free field. ArXiv preprint.

[100]    Schramm, O. and Wilson, D. B. (2005). SLE coordinate changes. New York J. Math. 11, 659–669 (electronic). http://nyjm.albany.edu:8000/j/2005/11_659.html. MR2188260 (2007e:82019)

[101]    Seymour, P. D. and Welsh, D. J. A. (1978). Percolation probabilities on the square lattice. Ann. Discrete Math. 3, 227–245. Advances in graph theory (Cambridge Combinatorial Conf., Trinity College, Cambridge, 1977). MR0494572 (58 #13410)

[102]    Sheffield, S. (2009). Exploration trees and conformal loop ensembles. Duke Math. J. 147, 1, 79–129. http://dx.doi.org/10.1215/00127094-2009-007. MR2494457 (2010g:60184)

[103]    Sheffield, S. and Werner, W. (2010). Conformal loop ensembles: The Markovian characterization and the loop-soup construction. To appear, Ann. of Math.

[104]    Sheffield, S. and Wilson, D. B. (2010). Schramm’s proof of Watts’ formula. ArXiv preprint.

[105]    Smirnov, S. (2001). Critical percolation in the plane: conformal invariance, Cardy’s formula, scaling limits. C. R. Acad. Sci. Paris Sér. I Math. 333, 3, 239–244. http://dx.doi.org/10.1016/S0764-4442(01)01991-7. MR1851632 (2002f:60193)

[106]    Smirnov, S. (2005). Critical percolation and conformal invariance. In XIVth International Congress on Mathematical Physics. World Sci. Publ., Hackensack, NJ, 99–112. MR2227824 (2007h:82030)

[107]    Smirnov, S. (2006). Towards conformal invariance of 2D lattice models. In International Congress of Mathematicians. Vol. II. Eur. Math. Soc., Zürich, 1421–1451. MR2275653 (2008g:82026)

[108]    Smirnov, S. (2009). Critical percolation in the plane. ArXiv preprint.

[109]    Smirnov, S. (2010a). Conformal invariance in random cluster models. I. Holomorphic fermions in the Ising model. Ann. of Math. (2) 172, 2, 1435–1467. http://dx.doi.org/10.4007/annals.2010.172.1441. MR2680496

[110]    Smirnov, S. (2010b). Discrete complex analysis and probability. ArXiv preprint.

[111]    Smirnov, S. (2011). Conformal invariance in random cluster models. II. Scaling limit of the interface. In preparation.

[112]    Stauffer, D. and Aharony, A. (1992). Introduction to percolation theory, 2nd ed. Taylor & Francis, London.

[113]    Stein, E. M. and Shakarchi, R. (2003a). Complex analysis. Princeton Lectures in Analysis, II. Princeton University Press, Princeton, NJ. MR1976398 (2004d:30002)

[114]    Stein, E. M. and Shakarchi, R. (2003b). Fourier analysis. Princeton Lectures in Analysis, Vol. 1. Princeton University Press, Princeton, NJ. An introduction. MR1970295 (2004a:42001)

[115]    van den Berg, J. and Kesten, H. (1985). Inequalities with applications to percolation and reliability. J. Appl. Probab. 22, 3, 556–569. MR799280 (87b:60027)

[116]    Werner, W. (2004). Random planar curves and Schramm-Loewner evolutions. In Lectures on probability theory and statistics. Lecture Notes in Math., Vol. 1840. Springer, Berlin, 107–195. MR2079672 (2005m:60020)

[117]    Werner, W. (2009). Lectures on two-dimensional critical percolation. In Statistical mechanics. IAS/Park City Math. Ser., Vol. 16. Amer. Math. Soc., Providence, RI, 297–360. MR2523462 (2011e:82042)

[118]    Wilson, D. B. (2011). XOR-Ising loops and the Gaussian free field. ArXiv preprint.

[119]     Zhan, D. (2008). Duality of chordal SLE. Invent. Math. 174, 2, 309–353. http://dx.doi.org/10.1007/s00222-008-0132-z. MR2439609 (2010f:60239)

[120]    Zhan, D. (2010). Duality of chordal SLE, II. Ann. Inst. Henri Poincaré Probab. Stat. 46, 3, 740–759. http://dx.doi.org/10.1214/09-AIHP340. MR2682265