[1]    S. Adams, R. Kotecký and S. Müller, in preparation.

[2]    S. Alexander and R. Orbach (1982). Density of states on fractals: “fractons”. J. Phys. (Paris) Lett. 43, 625–631.

[3]    S. Andres, M.T. Barlow, J.-D. Deuschel and B.M. Hambly (2010). Invariance principle for the random conductance model, (preprint). MR2599199

[4]    D.G. Aronson (1967). Bounds for the fundamental solution of a parabolic equation. Bull. Amer. Math. Soc. 73, 890–896. MR0217444

[5]    M.T. Barlow (2004). Random walks on supercritical percolation clusters. Ann. Probab. 32, no. 4, 3024–3084. MR2094438

[6]    M.T. Barlow and J. Černý (2010). Convergence to fractional kinetics for random walks associated with unbounded conductances. Probab. Theory Rel. Fields 149, no. 3-4, 639–673. MR2776627

[7]    M.T. Barlow and J.-D. Deuschel (2010). Invariance principle for the random conductance model with unbounded conductances. Ann. Probab. 38, no. 1, 234–276. MR2599199

[8]    M.T. Barlow and B.M. Hambly (2009). Parabolic Harnack inequality and local limit theorem for percolation clusters. Electron. J. Probab. 14, no. 1, 1–27. MR2471657

[9]    I. Benjamini, H. Duminil-Copin, G. Kozma and A. Yadin (2011). Disorder, entropy and harmonic functions. arXiv:1111.4853

[10]    I. Benjamini and E. Mossel (2003). On the mixing time of a simple random walk on the super critical percolation cluster. Probab. Theory Rel. Fields 125, no. 3, 408–420. MR1967022

[11]    N. Berger and M. Biskup (2007). Quenched invariance principle for simple random walk on percolation clusters. Probab. Theory Rel. Fields 137, no. 1-2, 83–120. MR2278453

[12]    N. Berger, M. Biskup, C.E. Hoffman and G. Kozma (2008). Anomalous heat-kernel decay for random walk among bounded random conductances. Ann. Inst. Henri Poincaré 274, no. 2, 374–392. MR2446329

[13]    N. Berger and J.-D. Deuschel (2011). A quenched invariance principle for non-elliptic random walk in i.i.d. balanced random environments. arxiv:1108.3995.

[14]    M. Biskup, in preparation.

[15]    M. Biskup and O. Boukhadra (2010). Subdiffusive heat-kernel decay in four-dimensional i.i.d. random conductance models. J. Lond. Math. Soc. (to appear).

[16]     M. Biskup, O. Louidor, A. Rozinov and A. Vandenberg-Rodes (2011). Trapping in the random conductance model. (in preparation).

[17]    M. Biskup and R. Kotecký (2007). Phase coexistence of gradient Gibbs states. Probab. Theory Rel. Fields 139, no. 1–2, 1–39. MR2322690

[18]    M. Biskup and T.M. Prescott (2007). Functional CLT for random walk among bounded conductances. Electron. J. Probab. 12, Paper no. 49, 1323–1348. MR2354160

[19]    M. Biskup and H. Spohn (2011). Scaling limit for a class of gradient fields with non-convex potentials. Ann. Probab. 39 (2011), no. 1, 224–251. MR2778801

[20]    E. Bolthausen, J.-D. Deuschel and O. Zeitouni (2011). Recursions and tightness for the maximum of the discrete, two dimensional Gaussian free field. Electron. Commun. Probab. 16, 114–119. MR2772390

[21]    O. Boukhadra (2010). Heat-kernel estimates for random walk among random conductances with heavy tail. Stoch. Process. Appl. 120, no. 2, 182–194. MR2576886

[22]    O. Boukhadra (2010). Standard spectral dimension for polynomial lower-tail random conductances model, Electron. Commun. Probab. 15, Paper no. 68, 2069–2086. MR2745726

[23]    B.M. Brown (1971). Martingale central limit theorems. Ann. Math. Statist. 42 59–66. MR0290428

[24]    S. Buckley (2011). Problems in Random Walks in Random Environments. DPhil thesis, University of Oxford.

[25]    R.M. Burton and M. Keane (1989). Density and uniqueness in percolation. Commun. Math. Phys. 121, no. 3, 501–505. MR0990777

[26]    P. Caputo, A. Faggionato and T. Prescott (2009). Invariance principle for Mott variable range hopping and other walks on point processes. arXiv:0912.4591 MR2538077

[27]    P. Caputo and D. Ioffe (2003). Finite volume approximation of the effective diffusion matrix: the case of independent bond disorder.  Ann. Inst. H. Poincaré Probab. Statist. 39, no. 3, 505–525. MR1978989

[28]    E.A. Carlen, S. Kusuoka, and D.W. Stroock (1987). Upper bounds for symmetric Markov transition functions. Ann. Inst. H. Poincaré Probab. Statist. 23, no. 2, suppl., 245–287. MR0898496

[29]    T.K. Carne (1985). A transmutation formula for Markov chains. Bull. Sci. Math. 109 399–405. MR0837740

[30]    J. Černý (2011). On two-dimensional random walk among heavy-tailed conductances. Elect. J. Probab. 16, Paper no. 10, pages 293–313. MR2771138

[31]    J.T. Chayes and L. Chayes (1986). Bulk transport properties and exponent inequalities for random resistor and flow networks. Commun. Math. Phys. 105, no. 1, 133–152. MR0847132

[32]    J. Cheeger (1970). A lower bound for the lowest eigenvalue of the Laplacian. In: R. C. Gunning, ed. Problems in Analysis: A Symposium in Honor of S. Bochner, Princeton Univ. Press, Princeton, N.J., pp. 195–199. MR0402831

[33]    F. Comets and S. Popov (2012). Ballistic regime for random walks in random environment with unbounded jumps and Knudsen billiards. Ann. Inst. Henri Poincaré Probab. et Stat. (to appear).

[34]    C. Cotar and J.-D. Deuschel (2011). Decay of covariances, uniqueness of ergodic component and scaling limit for a class of ∇φ systems with non-convex potential, arXiv:0807.2621

[35]    C. Cotar, J.-D. Deuschel and S. Müller (2009). Strict convexity of the free energy for a class of non-convex gradient models. Commun. Math. Phys. 286, no. 1, 359-376. MR2470934

[36]    Th. Coulhon and A. Grigor’yan (2003). Pointwise estimates for transition probabilities of random walks on infinite graphs. Fractals in Graz 2001, 119–134, Trends Math., Birkhäuser, Basel. MR2091701

[37]    O. Daviaud (2006). Extremes of the discrete two-dimensional Gaussian free field. Ann. Probab. 34 962–986. MR2243875

[38]    E.B. Davies (1989). Heat Kernels and Spectral Theory. Cambridge Univ. Press, Cambridge, UK. MR0990239

[39]    E.B. Davies (1993). Large deviations for heat kernels on graphs. J. London Math. Soc. (2) 47, no. 1, 65–72. MR1200978

[40]    E. De Giorgi (1957). Sulla differenziabilità e l’analiticità delle estremali degli integrali multipli regolari. Mem. Accad. Sci. Torino. Cl. Sci. Fis. Mat. Nat. (3) 3, 25–43. MR0093649

[41]    T. Delmotte (1999). Parabolic Harnack inequality and estimates of Markov chains on graphs. Rev. Mat. Iberoamericana 15, no. 1, 181–232. MR1681641

[42]    T. Delmotte and J.-D. Deuschel (2005). On estimating the derivatives of symmetric diffusions in stationary random environment, with applications to ∇ϕ interface model. Probab. Theory Rel. Fields 133, no. 3, 358–390. MR2198017

[43]    A. De Masi, P.A. Ferrari, S. Goldstein and W.D. Wick (1985). Invariance principle for reversible Markov processes with application to diffusion in the percolation regime. In: Particle Systems, Random Media and Large Deviations (Brunswick, Maine), pp. 71–85, Contemp. Math., 41, Amer. Math. Soc., Providence, RI. MR0814703

[44]    A. De Masi, P.A. Ferrari, S. Goldstein and W.D. Wick (1989). An invariance principle for reversible Markov processes. Applications to random motions in random environments. J. Statist. Phys. 55, no. 3-4, 787–855. MR1003538

[45]    A. Dembo and O. Zeitouni (2010). Large deviations techniques and applications, Corrected reprint of the second (1998) edition. Stochastic Modelling and Applied Probability, vol. 38. Springer-Verlag, Berlin. MR2571413

[46]    Y. Derriennic (2006). Some aspects of recent works on limit theorems in ergodic theory with special emphasis on the “central limit theorem”. Discrete Contin. Dyn. Syst. 15, no. 1, 143–158. MR2191389

[47]    Y. Derriennic and M. Lin (2003). The central limit theorem for Markov chains started at a point. Probab. Theory Related Fields 125, no. 1, 73–76. MR1952457

[48]    P.G. Doyle and J.L. Snell (1984). Random walks and electric networks. Carus Mathematical Monographs, 22. Mathematical Association of America, Washington, DC. MR0920811

[49]    L.E. Dubins (1968). On a theorem of Skorohod. Ann. Math. Statist. 39 2094–2097. MR0234520

[50]    H. Duminil-Copin (2009). Law of the Iterated Logarithm for the random walk on the infinite percolation cluster. arXiv:0809.4380

[51]    R. Durrett (2010). Probability: theory and examples. Fourth edition. Cambridge Series in Statistical and Probabilistic Mathematics. Cambridge University Press, Cambridge. MR2722836

[52]    J.C. Dyre and T.B. Schrèder (2000). Universality of ac conduction in disordered solids Rev. Mod. Phys. 72, 873–892.

[53]    R.G. Edwards and A.D.Sokal (1988). Generalization of the Fortuin-Kasteleyn-Swendsen-Wang representation and Monte Carlo algorithm. Phys. Rev. D (3) 38, no. 6, 2009–2012. MR0965465

[54]    G. Faraud (2011). A central limit theorem for random walk in a random environment on a marked Galton-Watson tree. Electron. J. Prob. 16, Paper no. 6. MR2754802

[55]    T. Funaki (2005). Stochastic Interface Models. In.: J. Picard (ed.), Lectures on probability theory and statistics, Lecture Notes in Mathematics, vol. 1869, Springer-Verlag, Berlin. MR2227242

[56]    T. Funaki and H. Spohn (1997). Motion by mean curvature from the Ginzburg-Landau ∇ϕ interface model. Commun. Math. Phys. 185, no. 1, 1–36. MR1463032

[57]    E.B. Fabes and D.W. Stroock (1986). A new proof of the Moser’s parabolic Harnack inequality via the old ideas of Nash. Arch. Ration. Mech. Anal. 96, 327–338. MR0855753

[58]    P. Ferrari, R.M. Grisi, P. Groisman (2010). Harmonic deformation of Delaunay triangulations. arXiv:1012.1677

[59]    L.R.G. Fontes and P. Mathieu (2006). On symmetric random walks with random conductances on ℤ^d. Probab. Theory Rel. Fields 134, no. 4, 565–602. MR2214905

[60]    C.M. Fortuin and P.W. Kasteleyn (1972). On the random-cluster model. I. Introduction and relation to other models. Physica 57, 536–564. MR0359655

[61]    C. Gallesco, N. Gantert, S. Popov and M. Vachovskaia (2011). A conditional quenched CLT for random walks among random conductances on ℤ^d. arXiv:1108.5616

[62]    C. Gallesco and S. Popov (2010). Conditional and uniform quenched CLTs for one-dimensional random walks among random conductances. arXiv:1011.1196

[63]    N. Gantert, S. Müller, S. Popov and M. Vachovskaia (2011). Random walks on Galton-Watson trees with random conductances. arXiv:1101.2769

[64]    G. Giacomin (2002). Limit theorems for random interface models of Ginzburg-Landau ∇φ type. Stochastic partial differential equations and applications (Trento, 2002), 235–253, Lecture Notes in Pure and Appl. Math., 227, Dekker, New York. MR1919512

[65]    G. Giacomin, S. Olla and H. Spohn (2001). Equilibrium fluctuations for ∇φ interface model. Ann. Probab. 29, no. 3, 1138–1172. MR1872740

[66]    A. Gloria and J.-C. Mourrat (2011). Quantitative version of Kipnis-Varadhan’s theorem and Monte-Carlo approximation of homogenized coefficients. arXiv:1103.4591

[67]    A. Gloria and F. Otto (2011). An optimal variance estimate in stochastic homogenization of discrete elliptic equations. Ann. Probab. 39, no. 3, 779–856. MR2789576

[68]    M.I. Gordin (1969). The central limit theorem for stationary processes. Dokl. Akad. Nauk SSSR 188 739–741. MR0251785

[69]    M.I. Gordin and B.A. Lifšic (1981). A remark about a Markov process with normal transition operator. In: Third Vilnius Conference on Probability and Statistics 1, 147–148.

[70]    A. Grigor’yan (1994). Heat kernel upper bounds on a complete non-compact manifold. Rev. Mat. Iberoamericana 10, no. 2, 395–452. MR1286481

[71]    A. Grigor’yan (2010). Heat kernels on metric measure spaces with regular volume growth. Handbook of geometric analysis, No. 2, 1–60, Adv. Lect. Math. (ALM), 13, Int. Press, Somerville, MA. MR2743439

[72]    G.R. Grimmett (1999). Percolation (Second edition), Grundlehren der Mathematischen Wissenschaften, vol. 321. Springer-Verlag, Berlin. MR1707339

[73]    G. Grimmett (2006). The random-cluster model. Grundlehren der Mathematischen Wissenschaften, vol. 333. Springer-Verlag, Berlin. MR2243761

[74]    G. Grimmett and H. Kesten (1984). First-passage percolation, network flows and electrical resistances. Z. Wahrsch. Verw. Gebiete 66, no. 3, 335–366. MR0751574

[75]    G.R. Grimmett, H. Kesten, and Y. Zhang (1993). Random walk on the infinite cluster of the percolation model. Probab. Theory Rel. Fields 96, no. 1, 33–44. MR1222363

[76]    G.R. Grimmett and J.M. Marstrand (1990). The supercritical phase of percolation is well behaved. Proc. Roy. Soc. London Ser. A 430, no. 1879, 439–457. MR1068308

[77]    X. Guo and Ofer Zeitouni (2010). Quenched invariance principle for random walks in balanced random environment Probab. Theory Relat. Fields (to appear).

[78]    D. Heicklen and C. Hoffman (2005). Return probabilities of a simple random walk on percolation clusters. Electron. J. Probab. 10, no. 8, 250–302. MR2120245

[79]    F. den Hollander (2000). Large deviations. Fields Institute Monographs, vol 14., American Mathematical Society, Providence, RI, x+143 pp. MR1739680

[80]    I. Horváth, B. Tóth, B. Vet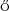 (2011). Diffusive limit for the myopic self-avoiding random walk in d ≥ 3. Probab. Theory Relat. Fields (to appear). MR2754400

[81]    X. Hu, J. Miller and Y. Peres (2010). Thick points of the Gaussian free field. Ann. Probab. 38, 896–926. MR2642894

[82]    M. Jerrum and A. Sinclair (1988). Conductance and the rapid mixing property for Markov chains: the approximation of the permanent resolved. Proc. of the 20th Annual ACM Symposium on Theory of Computing (STOC 1988), 235–243.

[83]    V.V. Jikov, S.M. Kozlov and O.A. Oleinik (1994). Homogenization of differential operators and integral functionals, Springer-Verlag, Berlin, pp. 570. MR1329546

[84]    K. Kawazu and H. Kesten (1984). On birth and death processes in symmetric random environment. J. Statist. Phys. 37, no. 5-6, 561–576. MR0775792

[85]    H. Kesten (1982). Percolation theory for mathematicians. Progress in Probability and Statistics, vol. 2. Birkhäuser, Boston, Mass., iv+423 pp. MR0692943

[86]    C. Kipnis and S.R.S. Varadhan (1986). A central limit theorem for additive functionals of reversible Markov processes and applications to simple exclusions. Commun. Math. Phys. 104, no. 1, 1–19. MR0834478

[87]    G. Kirchhoff (1847). Ueber die Auflösung der Gleichungen, auf welche man bei der Untersuchung der linearen Vertheilung galvanischer Ströme geführt wird. Ann. Phys. Chem. 72, no. 12, 497–508.

[88]    J. Klicnarová and D. Volný (2009). On the exactness of the Wu-Woodroofe approximation. Stochastic Process. Appl. 119, no. 7, 2158–2165. MR2531087

[89]    S.M. Kozlov (1985). The averaging method and walks in inhomogeneous environments. Uspekhi Mat. Nauk 40, no. 2(242), 61–120. MR0786087

[90]    T. Kumagai (2010). Random walks on disordered media and their scaling limits. St. Flour lecture notes (to appear).

[91]    R. Künnemann (1983). The diffusion limit for reversible jump processes on ℤ^d with ergodic random bond conductivities. Commun. Math. Phys. 90, no. 1, 27–68. MR0714611

[92]    G.F. Lawler (1982/83). Weak convergence of a random walk in a random environment. Commun. Math. Phys. 87, no. 1, 81–87. MR0680649

[93]    G.F. Lawler (1991). Intersections of random walks. Probability and its Applications. Birkhüser Boston, Inc., Boston, MA, 219 pp. MR1117680

[94]    G. Lawler and A. Sokal (1988). Bounds on the L² spectrum for Markov chains and Markov processes: a generalization of Cheeger’s inequality, Trans. Amer. Math. Soc. 309, 557–580. MR0930082

[95]    T.M. Liggett (2010). Continuous time Markov processes. An introduction. Graduate Studies in Mathematics, vol. 113. American Mathematical Society, Providence, RI. MR2574430

[96]    T.M. Liggett, R.H. Schonmann and A.M. Stacey (1997). Domination by product measures. Ann. Probab. 25, no. 1, 71–95. MR1428500

[97]    L. Lovász and R. Kannan (1999). Faster mixing via average conductance. Annual ACM Symposium on Theory of Computing (Atlanta, GA, 1999), 282–287, ACM, New York. MR1798047

[98]    R. Lyons, R. Pemantle and Y Peres (1996). Biased random walks on Galton-Watson trees. Probab. Theory Rel. Fields 106, no. 2, 249–264. MR1410689

[99]    B. Morris and Y. Peres (2005). Evolving sets, mixing and heat kernel bounds. Probab. Theory Rel. Fields 133, no. 2, 245–266. MR2198701

[100]    P. Mathieu (2008). Quenched invariance principles for random walks with random conductances. J. Statist. Phys. 130, no. 5, 1025–1046. MR2384074

[101]    P. Mathieu and A.L. Piatnitski (2007). Quenched invariance principles for random walks on percolation clusters. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 463 2287–2307. MR2345229

[102]    P. Mathieu and E. Remy (2004). Isoperimetry and heat kernel decay on percolation clusters. Ann. Probab. 32, no. 1A, 100–128. MR2040777

[103]    M. Maxwell and M. Woodroofe (2000). Central limit theorems for additive functionals of Markov chains. Ann. Probab. 28, 713–724. MR1782272

[104]    J. Miller (2010). Universality for SLE(4). arXiv:1010.1356

[105]    R. Montenegro and P. Tetali (2006). Mathematical aspects of mixing times in Markov chains. Found. Trends Theor. Comput. Sci. 1, no. 3, x+121 pp. MR2341319

[106]    J.-C. Mourrat (2011). A quantitative central limit theorem for the random walk among random conductances. arXiv:1105.4485 MR2841076

[107]    A. Naddaf and T. Spencer (1997). On homogenization and scaling limit of some gradient perturbations of a massless free field. Commun. Math. Phys. 183, no. 1, 55–84. MR1461951

[108]    A. Nachmias and G. Kozma (2009). The Alexander-Orbach conjecture holds in high dimensions. Invent. Math. 178, no. 3, 635–654. MR2551766

[109]    J. Nash (1958). Continuity of solutions of parabolic and elliptic equations. Am. J. Math. 80, 931–954. MR0100158

[110]    S. Olla (2001). Central limit theorems for tagged particles and for diffusions in random environment. In: F. Comets, É. Pardoux (eds): Milieux alátoires Panor. Synthèses 12, Soc. Math. France, Paris. MR2226846

[111]    H. Owhadi (2003). Approximation of the effective conductivity of ergodic media by periodization. Probab. Theory Related Fields 125, no. 2, 225–258. MR1961343

[112]    G. Papanicolaou and S.R.S. Varadhan (1982). Diffusions with random coefficients. In: Statistics and Probability: Essays in Honor of C.R. Rao, North-Holland, Amsterdam, pp. 547–552. MR0659505

[113]    M. Peligrad and S. Utev (2006). Central limit theorem for stationary linear processes. Ann. Probab. 34, no. 4, 1608–1622. MR2257658

[114]    Y. Peres and O. Zeitouni (2008). A central limit theorem for biased random walks on Galton- Watson trees. Probab. Theory Rel. Fields 140, no. 3-4, 595–629. MR2365486

[115]    G. Pete (2008). A note on percolation on ℤ^d: Isoperimetric profile via exponential cluster repulsion. Electron. Commun. Probab. 13, 377–392. MR2415145

[116]    K. Petersen (1989). Ergodic theory. Petersen, Karl Ergodic theory. Corrected reprint of the 1983 original. Cambridge Studies in Advanced Mathematics, vol 2. Cambridge University Press, Cambridge. MR1073173

[117]    J. Quastel (1992). Diffusion of color in the simple exclusion process. Commun. Pure Appl. Math. 45, no. 6, 623–679. MR1162368

[118]    C. Rau (2007). Sur le nombre de points visités par une marche aléatoire sur un amas infini de percolation, Bull. Soc. Math. France vol. 135, no. 1, 135–169. MR2430203

[119]    O. Schramm and S. Sheffield (2009). Contour lines of the two-dimensional discrete Gaussian free field. Acta Math. 202, no. 1, 21–137. MR2486487

[120]    T.B. Schrèder and J.C. Dyre (2008). ac hopping conduction at extreme disorder takes place on the percolating cluster. Phys. Rev. Lett. 101, no. 2, 025901.

[121]    S. Sethuraman, S.R.S. Varadhan and H-T. Yau (2000). Diffusive limit of a tagged particle in asymmetric simple exclusion processes. Comm. Pure Appl. Math. 53, 972–1006. MR1755948

[122]    S. Sheffield, Random Surfaces, Astérisque No. 304, (2005), 175 pp. MR2251117

[123]    S. Sheffield (2007). Gaussian free field for mathematicians. Probab. Theory Rel. Fields 139, no. 3-4, 521–541. MR2322706

[124]    V. Sidoravicius and A.-S. Sznitman (2004). Quenched invariance principles for walks on clusters of percolation or among random conductances. Probab. Theory Rel. Fields 129, no. 2, 219–244. MR2063376

[125]    A.V. Skorohod (1961). Issledovaniya po teorii sluchainykh protsessov. Izdat. Kiev. Univ., Kiev, 216 pp. MR0185619

[126]    F. Spitzer (1976). Principles of Random Walks. Second edition. Graduate Texts in Mathematics, Vol. 34. Springer-Verlag, New York-Heidelberg, xiii+408 pp. MR0388547

[127]    V. Strassen (1967). Almost sure behavior of sums of independent random variables and martingales. Proc. Fifth Berkeley Sympos. Math. Statist. and Probability (Berkeley, Calif., 1965/66), vol. II: Contributions to Probability Theory, Part 1, pp. 315–343, Univ. California Press, Berkeley, Calif. MR0214118

[128]    A. Telcs (2010). Diffusive limits on the Penrose tiling. J. Stat. Phys. 141, no. 4, 661–668. MR2733400

[129]    N.Th. Varopoulos (1985). Long range estimates for Markov chains, Bull. Sci. Math. 109 225–252. MR0822826

[130]    N.Th. Varopoulos (1985). Isoperimetric inequalities and Markov chains. J. Funct. Anal. 63, no. 2, 215–239. MR0803093

[131]    N. Varopoulos, L. Saloff-Coste and T. Coulhon (1992). Analysis and Geometry on Groups. Cambridge Univ. Press, Cambridge, UK. MR1218884

[132]    Y. Velenik, Localization and delocalization of random interfaces. Probab. Surveys 3 (2006) 112–169. MR2216964

[133]    D. Volný (2010). Martingale approximation and optimality of some conditions for the central limit theorem. J. Theoret. Probab. 23, no. 3, 888–903. MR2679961

[134]    J. Wehr (1997). A lower bound on the variance of conductance in random resistor networks. J. Statist. Phys. 86, no. 5-6, 1359–1365. MR1450770

[135]    W. Woess (2000). Random walks on infinite graphs and groups. Cambridge Tracts in Mathematics vol. 138, Cambridge University Press. MR1743100

[136]    A. Yadin and A. Yehudayoff (2011). Loop-erased random walk and Poisson kernel on planar graphs. Ann. Probab. 39, no. 4, 1243–1285.