[1]    Aleshkyavichene, A. K. (1979). Probabilities of large deviations for the maximum of sums of independent random variables. Theory Probab. Appl., 24, 16–33. MR0522234

[2]    Aleshkyavichene, A. K. (1979). Probabilities of large deviations for the maximum of sums of independent random variables. II. Theory Probab. Appl., 24, 318–331. MR0532445

[3]    Anderson, T. W. (2003). An Introduction to Multivariate Statistical Analysis. Third edition. Wiley-Interscience. MR1990662

[4]    Arvesen, J. N. (1969). Jackknifing U-statistics. Ann. Math. Statist., 40, 2076–2100. MR0264805

[5]    Balan, R. and Kulik, R. (2009). Weak invariance principle for mixing sequences in the domain of attraction of normal law. Studia Sci. Math. Hungar., 46, 329–343. MR2657020

[6]    Bentkus, V., Bloznelis, M. and Götze, F. (1996). A Berry-Esséen bound for Student’s statistic in the non-i.i.d. case. J. Theoret. Probab., 9, 765–796. MR1400598

[7]    Bentkus, V. and Götze, F. (1996). The Berry-Esséen bound for Student’s statistic. Ann. Probab., 24, 491–503. MR1387647

[8]    Bentkus, V., Jing, B.-Y., Shao, Q.-M. and Zhou, W. (2007). Limit distributions of non-central t-statistic and their applications to the power of t-test under non-normality. Bernoulli, 13, 346–364. MR2331255

[9]    Bloznelis, M. and Putter, H. (1998). One term Edgeworth expansion for Student’s t statistic. Probability Theory and Mathematical Statistics: Proceedings of the Seventh Vilnius Conference (B. Grigelionis et al., eds.), Vilnius, Utrecht: VSP/TEV, 1999, 81–98.

[10]    Bloznelis, M. and Putter, H. (2002). Second order and Bootstrap approximation to Student’s statistic. Theory Probab. Appl., 47, 374–381. MR2003205

[11]    Chistyakov, G. P. and Götze, F. (2003). Moderate deviations for Student’s statistic. Theory Probab. Appl., 47, 415–428. MR1975426

[12]    Chistyakov, G. P. and Götze, F. (2004a). On bounds for moderate deviations for Student’s statistic. Theory Probab. Appl., 48, 528–535. MR2141355

[13]    Chistyakov, G. P. and Götze, F. (2004b). Limit distributions of Studentized means. Ann. Probab., 32, no. 1A, 28–77. MR2040775

[14]    Choi, Y.-K. and Moon, H.-J. (2010). Self-normalized weak limit theorems for a ϕ-mixing sequence. Bull. Korean Math. Soc., 47, 1139–1153. MR2560606

[15]    Csörg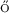, M. and Horváth, L. (1988). Asymptotic representations of self-normalized sums. Probability and Mathematical Statistics, 9, no. 1, 15–24. MR0945676

[16]    Csörg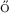, M. and Hu, Z. (2013). A strong approximation of self-normalized sums. Sci. China Math., 56, 149–160. MR3016589

[17]    Csörg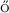, M., Hu, Z. and Mei, H. (2013). Strassen-type law of the iterated logarithm for self-normalized sums. J. Theoret. Probab., 26, 311–328. MR3055805

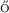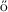[18]    Csörg, M., Szyszkowicz, B. and Wang, Q. (2003a). Darling-Erds theorems for self-normalized sums. Ann. Probab., 31, 676–692. MR1964945

[19]    Csörg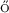, M., Szyszkowicz, B. and Wang, Q. (2003b). Donsker’s theorem for self-normalized partial sums processes. Ann. Probab., 31, 1228–1240. MR1988470

[20]    Csörg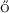, M., Szyszkowicz, B. and Wang, Q. (2004). On weighted approxiamtions and strong limit theorems for self-normalized partial sums processes. In Asymptotics Methods in Stochastics: Festschrift for M. Csörgö (L. Horváth and B. Szyszkowicz, eds.), Fields institute communications (Vol. 44), 489–521. MR2108953

[21]    Csörg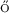, M., Szyszkowicz, B. and Wang, Q. (2008). On weighted approximations in D[0;1] with applications to self-normalized partial sum processes. Acta Math. Hungar., 121, 333–357. MR2461439

[22]    de la Peña, V., Lai, T. L. and Shao, Q. M. (2009). Self-normalized Processes: Theory and Statistical Applications. Springer, New York. MR2488094

[23]    Dembo, A. and Shao, Q.-M. (1998). Self-normalized moderate deviations and LILs. Stochastic Process. Appl., 75, 51–65. MR1629018

[24]    Dembo, A. and Shao, Q.-M. (2006). Large and moderate deviations for Hotelling’s t²-statistic. Elect. Comm. in Probab., 11, 149–159. MR2240708

[25]    Efron, B. (1969). Student’s t-test under symmetry conditions. J. Amer. Statist. Assoc., 1278–1302. MR0251826

[26]    Egorov, V. A. (1996). On the asymptotic behavior of self-normalized sums of random variables, Teor. Veroyatnost. i Primenen., 41, 643–650. MR1450081

[27]    Egorov, V. A. (2002). An estimate for the tail of the distribution of normalized and self-normalized sums. J. Math. Sci. (N. Y.), 127, 1717–1722. MR1976748

[28]    Einmahl, U. (1989). The Darling-Erds theorem for sums of i.i.d. random variables, Probab. Th. Rel. Fields, 82, 241–257. MR0998933

[29]    Giné, E., Götze, F. and Mason, D. (1997). When is the Student t-statistic asymptotically standard normal? Ann. Probab., 25, 1514–1531. MR1457629

[30]    Giné, E. and Mason, D. (1998). On the LIL for self-normalized sums of iid random variables. J. Theoret. Probab., 18, 351–370. MR1622575

[31]    Griffin, P. S. and Kuelbs, J. D. (1989). Self-normalized laws of the iterated logarithm. Ann. Probab., 17, 1571–1601. MR1048947

[32]    Griffin, P. S. and Mason, D. M. (1991). On the asymptotic normality of self-normalized sums. Math. Proc. Cambridge Philos. Soc., 109, 597–610. MR1094756

[33]    Hall, P. (1987). Edgeworth expansion for Student’s t statistic under minimal moment conditions. Ann. Probab., 15, 920–931. MR0893906

[34]    Hall, P. (1988). On the effect of random norming on the rate of convergence in the central limit theorem. Ann. Probab., 16, 1265–1280. MR0942767

[35]    Hall, P. and Wang, Q. (2004). Exact convergence rate and leading term in central limit theorem for student’s t statistic. Ann. Probab., 32, 1419–1437. MR2060303

[36]    Hu, Z., Shao, Q.-M. and Wang, Q. (2009). Cramér type large deviations for the maximum of self-normalized sums. Electronic Jour. of Probab., 14, 1181–1197. MR2511281

[37]    Jing, B.-Y., Shao, Q.-M. and Wang, Q. (2003). Self-normalized Cramér-type large deviations for independent random variables. Ann. Probab., 31, 2167–2215. MR2016616

[38]    Jing, B.-Y., Shao, Q.-M. and Zhou, W. (2004). Saddlepoint approximation for Student’s t-statistic with no moment conditions. Ann. Statist., 6, 2679–2711. MR2153999

[39]    Jing, B.-Y., Shao, Q.-M. and Zhou, W. (2008). Towards a universal self-normalized moderate deviation. Trans. Amec. Math. Soci., 360, 4263–4285. MR2395172

[40]    Kulik, R. (2006). Limit theorems for self-normalized linear processes. Statist. Probab. Lett., 76, 1947–1953. MR2329238

[41]    Lai, T. L., Shao, Q.-M., and Wang, Q. (2011). Cramér type moderate deviations for Studentized U-statistics. ESAIM – Probability and Statistics, 15, 168–179. MR2870510

[42]    Liu, W. and Shao, Q.-M. (2012). Cramér moderate deviation for Hotelling’s T² statistic with applications to global tests. Preprint.

[43]    Liu, W., Shao, Q.-M. and Wang, Q. (2012). Self-normalized Cramér type moderate deviations for the maximum of sums. Bernoulli, forthcoming. MR3079304

[44]    Logan, B. F., Mallows, C. L., Rice, S. O. and Sheep, L. A. (1973). Limit distributions of self-normalized sums. Ann. Probab., 1, 788–809. MR0362449

[45]    Maller, R. A. (1981). A theorem on products of random variables with application to regression. Australian Journal of Statistics, 23, 177–185. MR0636133

[46]    Mason, D. M. (2005). The asymptotic distribution of self-normalized triangular arrys. Journal of Theoret. Probab., 18, 853–870. MR2289935

[47]    Novak, S. Y. (2004). On self-normalized sums of random variables and the Student’s statistic. Theory Probab. Appl., 49, 336–344. MR2144306

[48]    O’Brien, G. L. (1980). A limit theorem for sample maxima and heavy branches in Galton-Watson trees. J. Appl. Probab., 17, 539–545. MR0568964

[49]    De la Pena, V. H. and Giné, E. (1999). Decoupling: From Dependence to Independence. Springer, New York. MR1666908

[50]    De la Pena, V. H., Klass, M. J. and Lai, T. L. (2000). Moment bounds for self-normalized martingales. In High Dimensional Probability II (E. Giné, D. M. Mason and J. A. Wellner, eds.), Birkhauser, Boston, 1–11. MR1857343

[51]    De la Pena, V. H., Klass, M. J. and Lai, T. L. (2004). Self-normalized processes: exponential inequalities, moment bounds and iterated logarithm laws. Ann. Probab., 32, 1902–1933. MR2073181

[52]    De la Pena, V. H., Lai, T. L. and Shao, Q.-M. (2009). Self-normalized Processes: Limit Theorey and Statistical Applications. Springer, New York. MR2488094

[53]    Prohorov, Yu. V. (1956). Covergence of random processes and limit theorems in probability theory. Theor. Probab. Appl., 1, 157–214. MR0084896

[54]    Robinson, J. and Wang, Q. (2005). On the self-normalized Cramér-type large deviation. Journal of Theoret. Probab., 18, 891–909. MR2300002

[55]    Shao, Q.-M. (1997). Self-normalized large deviations. Ann. Probab., 25, 285–328. MR1428510

[56]    Shao, Q.-M. (1998). Recent development in self-normalized limit theorems. In: Asymptotic Methods in Probability and Statistics (B. Szyszkowicz, ed.), Elsevier Science, 467–480. MR1661499

[57]    Shao, Q.-M. (1999). A Cramér type large deviation result for Student’s t-statistic. J. Theoret. Probab., 12, 385–398. MR1684750

[58]    Shao, Q.-M. (2004). Recent progress on self-normalized limit theorems. In: Probability, Finance And Insurance, World Sci. Publ., River Edge, NJ, 50–68. MR2189198

[59]    Shao, Q.-M. (2005). An explicit Berry-Esseen bound for Student’s t-statistic via Stein’s method. In Stein’s Method and Applications, Lect. Notes Ser. Inst. Math. Sci. Natl. Univ. Singap., 5, Singapore Univ. Press, Singapore, 143–155. MR2205333

[60]    Shao, Q.-M. (2010). Stein’s method, self-normalized limit theory and applications. In Proceedings of the International Congress of Mathematicians, Hyderabad, India, 1–25.

[61]    Shao, Q. M. and Zhou, W. (2012). Cramér type moderate deviation theorems for Studentized non-linear statistics. Preprint.

[62]    Shao, Q. M., Zhang, K. and Zhou, W. (2012). Berry-Esseen bounds for Studentized non-linear statistics via Stein’s method. Preprint.

[63]    Slavov, V. V. (1985). On the Berry-Esseen bound for Student’s statistic. In Stability Problems for Stochastic Models (V. V. Kalashnikov and V. M. Zolotarev, eds.), Lecture Notes in Math., 1155, Springer, Berlin, 355–390. MR0825335

[64]    Sepanski, S. (1994). Asymptotics for Multivariate t-statistic and Hotelling’s T²-statistic under infinite second moments via bootstrapping. J. Multivariate Anal., 49, 41–54. MR1275042

[65]     Wang, Q. (2004). On Darling Erdös type theorems for self-nornmalized sums, In Asymptotic Methods in Stochastics: Festschrift for Miklos Csorgo (Lajos Horvath and Barbara Szyszkowicz, eds.), International Conference on Asymptotic Methods in Stochastics. Fields Institute Communications, American Mathematical Society, 523–530. MR2108954

[66]    Wang, Q. (2005). Limit theorems for self-normalized large deviation. Electronic Journal of Probab., 10, 1260–1285. MR2176384

[67]    Wang, Q. (2011). Refined self-normalized large deviations for independent random variables. Journal of Theor. Probab., 24, 307–329. MR2795041

[68]    Wang, Q. and Hall, P. (2009). Relative errors in central limit theorem for Student’s t statistic, with applications. Statistica Sinica, 19, 343–354. MR2487894

[69]    Wang, Q. and Jing, B.-Y. (1999). An exponential nonuniform Berry-Esseen bound for self-normalized sums. Ann. Probab., 27, 2068–2088. MR1742902

[70]    Wang, Q., Jing, B.-Y. and Zhao, L. (2000). The Berry-Esseen bound for Studentized statistics. Ann. Probab., 28, 511–535. MR1756015

[71]    Zhou, W. and Jing, B.-Y. (2006). Tail probability approximations for Student’s t statistics. Probab. Theory Relat. Fields, 136, 541–559. MR2257135