4.3 The coset structure of vacuum gravity
For many applications, in particular for the black hole uniqueness theorems, it is of crucial importance
that the one-form  can be replaced by a function (twist potential). We have already pointed
out that
can be replaced by a function (twist potential). We have already pointed
out that  , parametrizing the non-static part of the metric, enters the effective action (9)
only via the field strength,
, parametrizing the non-static part of the metric, enters the effective action (9)
only via the field strength,  . For this reason, the variational equation for
. For this reason, the variational equation for  (that
is, the off-diagonal Einstein equation) assumes the form of a source-free Maxwell equation,
By virtue of Eq. (10), the (locally defined) function
(that
is, the off-diagonal Einstein equation) assumes the form of a source-free Maxwell equation,
By virtue of Eq. (10), the (locally defined) function 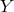 is a potential for the twist one-form,
is a potential for the twist one-form, 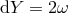 .
In order to write the effective action (9) in terms of the twist potential
.
In order to write the effective action (9) in terms of the twist potential 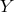 , rather than the one-form
, rather than the one-form  ,
one considers
,
one considers  as a fundamental field and imposes the constraint
as a fundamental field and imposes the constraint 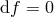 with the Lagrange
multiplier
with the Lagrange
multiplier 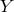 . The variational equation with respect to
. The variational equation with respect to 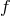 then yields
then yields 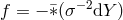 , which is used
to eliminate
, which is used
to eliminate 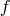 in favor of
in favor of 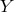 . One finds
. One finds 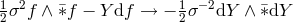 . Thus, the action (9)
becomes
where we recall that
. Thus, the action (9)
becomes
where we recall that 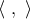 is the inner product with respect to the three-metric
is the inner product with respect to the three-metric 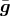 defined in
Eq. (8).
defined in
Eq. (8).
The action (12) describes a harmonic mapping into a two-dimensional target space, effectively coupled
to three-dimensional gravity. In terms of the complex Ernst potential 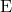 [52
[52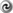 , 53
, 53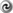 ], one has
], one has
The stationary vacuum equations are obtained from variations with respect to the three-metric
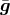 [
[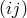 -equations] and the Ernst potential
-equations] and the Ernst potential 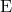 [
[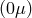 -equations]. One easily finds
-equations]. One easily finds
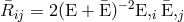 and
and 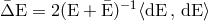 , where
, where 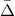 is the Laplacian with respect to
is the Laplacian with respect to
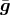 .
.
The target space for stationary vacuum gravity, parametrized by the Ernst potential 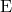 , is a
Kähler manifold with metric
, is a
Kähler manifold with metric 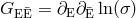 (see [62] for details). By virtue of the mapping
(see [62] for details). By virtue of the mapping
the semi-plane where the Killing field is time-like, 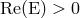 , is mapped into the interior of the complex unit
disc,
, is mapped into the interior of the complex unit
disc, 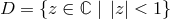 , with standard metric
, with standard metric 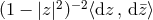 . By virtue of the stereographic
projection,
. By virtue of the stereographic
projection, 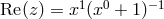 ,
, 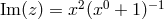 , the unit disc
, the unit disc 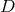 is isometric to the pseudo-sphere,
is isometric to the pseudo-sphere,
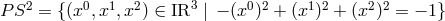 . As the three-dimensional Lorentz group,
. As the three-dimensional Lorentz group, 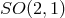 ,
acts transitively and isometrically on the pseudo-sphere with isotropy group
,
acts transitively and isometrically on the pseudo-sphere with isotropy group 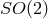 , the target space is the coset
, the target space is the coset
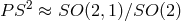 .
Using the universal covering
.
Using the universal covering 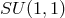 of
of 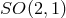 , one can parametrize
, one can parametrize 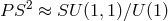 in
terms of a positive hermitian matrix
in
terms of a positive hermitian matrix 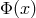 , defined by
Hence, the effective action for stationary vacuum gravity becomes the standard action for a
, defined by
Hence, the effective action for stationary vacuum gravity becomes the standard action for a 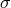 -model
coupled to three-dimensional gravity [139
-model
coupled to three-dimensional gravity [139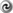 ],
],
The simplest nontrivial solution to the vacuum Einstein equations is obtained in the static, spherically
symmetric case: For 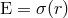 one has
one has 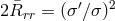 and
and 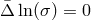 . With respect to the general
spherically symmetric ansatz
. With respect to the general
spherically symmetric ansatz
one immediately obtains the equations 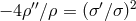 and
and 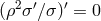 , the solution of which is the
Schwarzschild metric in the usual parametrization:
, the solution of which is the
Schwarzschild metric in the usual parametrization:  ,
, 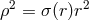 .
.
![]() ) describes a harmonic mapping into a two-dimensional target space, effectively coupled
to three-dimensional gravity. In terms of the complex Ernst potential
) describes a harmonic mapping into a two-dimensional target space, effectively coupled
to three-dimensional gravity. In terms of the complex Ernst potential ![]() [52
[52![]() , 53
, 53![]() ], one has
], one has
![]() , is a
Kähler manifold with metric
, is a
Kähler manifold with metric ![]() (see [62] for details). By virtue of the mapping
(see [62] for details). By virtue of the mapping
![]() one has
one has ![]() and
and ![]() . With respect to the general
spherically symmetric ansatz
. With respect to the general
spherically symmetric ansatz