A strictly increasing sequence of positive integers is called a
slightly curved sequence with small error
if the sequence can be well-approximated by a function whose second derivative goes to zero faster than or equal to
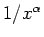
for some
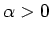
.
In this paper, we prove that arbitrarily long arithmetic progressions are contained in the graph of a slightly curved sequence with small error.
Furthermore, we extend Szemerédi's theorem to a theorem about
slightly curved sequences.
As a corollary,
it follows that the graph of the sequence
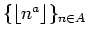
contains arbitrarily long arithmetic progressions
for every
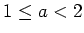
and every
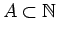
with positive upper
density.
Using this corollary, we show that
the set
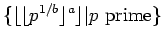
contains arbitrarily long arithmetic progressions for every
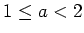
and
b>1.
We also prove that, for every

,
the graph of
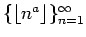
does not contain any arithmetic progressions of length 3.
Received October 22 2018; revised versions received February 21 2019;
February 22 2019.
Published in Journal of Integer Sequences,
February 22 2019.

