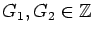
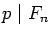
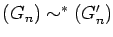
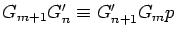
We consider a generalized Fibonacci sequence ( G_n ) by and G_n = G_n-1 + G_n-2 for any integer n. Let p be a prime number and let d(p) be the smallest positive integer n which satisfies . In this article, we introduce equivalence relations for the set of generalized Fibonacci sequences. One of the equivalence relations is defined as follows. We write if there exist integers m and n satisfying . 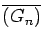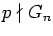We prove the following: if p ≡ 2 (mod 5), then the number of equivalence classes satisfying for any integer n is (p+1)/d(p)-1. If p ≡ ± 1 (mod 5), then the number is (p-1)/d(p)+1. Our results are refinements of a theorem given by Kôzaki and Nakahara in 1999. 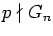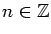They proved that there exists a generalized Fibonacci sequence ( G_n )such that for any if and only if one of the following three conditions holds: (1) p = 5; (2) p ≡ ± 1 (mod 5); (3) p ≡ 2 (mod 5) and d(p)<p+1.