 |
Journal of Integer Sequences, Vol. 18 (2015), Article 15.11.7 |
 |
Journal of Integer Sequences, Vol. 18 (2015), Article 15.11.7 |
Abstract:
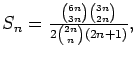 and the binomial coefficients
and the binomial coefficients
(Concerned with sequences
A000108
A001448
A001764
A005809
A048990
A176898.)
Received April 30 2015; revised version received December 16 2015. Published in Journal of Integer Sequences, December 16 2015.