Let

be a sequence of positive integers and
m a positive integer. We prove that "almost every" real quadratic unit
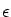
of norm (-1)
k admits at least
m distinct factorizations into a product of purely periodic irrationals of the form
Periods exhibited in this expression are not assumed minimal. The analogous assertion holds for real quadratic units
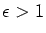
with prime trace and
m=1. The proofs are based on the fact that an integral polynomial map of the form
f(
x,
y)=
axy+
by+
cx+
d,
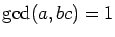
,
a>1,
b,
c>0, assumes almost every positive integral value and almost every prime value when evaluated over the positive integers.

