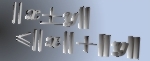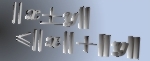| |
|
|
| |
Volume 9, Issue 1, Article 12 |
|
|
|
|
|
| |
Properties of Some Functions Connected to Prime Numbers
|
| |
|
Authors: |
Gabriel Mincu, Laurentiu Panaitopol, |
|
| |
|
Keywords:
|
Arithmetic functions, Inequalities, Landau's inequality, Additivity, Multiplicativity. |
|
| |
|
Date Received:
|
08/09/2007 |
|
| |
|
Date Accepted:
|
16/11/2007 |
|
| |
|
Subject Codes: |
11N64, 11Y70, 11N05.
|
|
| |
|
Editors: |
László Tóth, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
Let 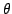 and and 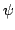 be the Chebyshev functions. We denote be the Chebyshev functions. We denote 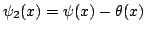 and and 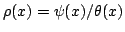 . We study subadditive and Landau-type properties for . We study subadditive and Landau-type properties for 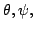 and and 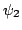 . We show that . We show that 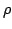 is subadditive and submultiplicative. Finally, we consider the prime counting function is subadditive and submultiplicative. Finally, we consider the prime counting function 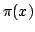 and show that and show that
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|