| |
|
|
| |
Volume 7, Issue 2, Article 74 |
|
|
|
|
|
| |
Hyers-Ulam stability of the Generalized Trigonometric Formulas
|
| |
|
Authors: |
Ahmed Redouani, Elhoucien Elqorachi, Belaid Bouikhalene, |
|
| |
|
Keywords:
|
Locally compact group, Functional equation, Hyers-Ulam stability, Superstability. |
|
| |
|
Date Received:
|
14/09/05 |
|
| |
|
Date Accepted:
|
14/11/05 |
|
| |
|
Subject Codes: |
39B42, 39B32.
|
|
| |
|
Editors: |
Themistocles M. Rassias, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
In this paper, we will investigate the Hyers-Ulam stability of the following functional equations
and
where 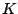 is a compact subgroup of morphisms of is a compact subgroup of morphisms of  , ,  is a normalized Haar measure of is a normalized Haar measure of 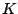 , ,  is a complex is a complex 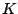 -invariant measure with compact support, the functions -invariant measure with compact support, the functions 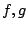 are continuous on are continuous on  and and 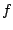 is assumed to satisfies the Kannappan type condition is assumed to satisfies the Kannappan type condition 
The paper of Székelyhidi [30] is the essential motivation for the present work and the methods used here are closely related to and inspired by those in [30].
The concept of the generalized Hyers-Ulam stability of mappings was introduced in the subject of functional equations by Th. M. Rassias in [20].
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|



