| |
|
|
| |
Volume 7, Issue 2, Article 57 |
|
|
|
|
|
| |
Relation Between Best Approximant and Orthogonality in $C_1$-classes
|
| |
|
Authors: |
Mecheri Salah, |
|
| |
|
Keywords:
|
Best approximant, Schatten $p$-classes, Orthogonality, $varphi$-Gateaux derivative. |
|
| |
|
Date Received:
|
21/05/05 |
|
| |
|
Date Accepted:
|
13/03/06 |
|
| |
|
Subject Codes: |
Primary 41A52, 41A35, 47B47; Secondary 4
|
|
| |
|
Editors: |
Gradimir V. Milovanovic, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
Let 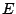 be a complex Banach space and let be a complex Banach space and let 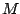 be subspace of be subspace of 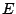 . In this paper we characterize the best approximant to . In this paper we characterize the best approximant to 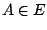 from from 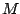 and we prove the uniqueness, in terms of a new concept of derivative. Using this result we establish a new characterization of the best- and we prove the uniqueness, in terms of a new concept of derivative. Using this result we establish a new characterization of the best-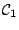 approximation to approximation to 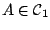 (trace class) from (trace class) from 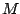 . Then, we apply these results to characterize the operators which are orthogonal in the sense of Birkhoff. . Then, we apply these results to characterize the operators which are orthogonal in the sense of Birkhoff.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|



