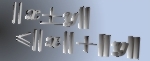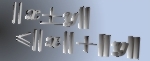| |
|
|
| |
Volume 7, Issue 1, Article 30 |
|
|
|
|
|
| |
An Extended Hardy-Hilbert Inequality and Its Applications
|
| |
|
Authors: |
Weijian Jia, Mingzhe Gao, |
|
| |
|
Keywords:
|
Power-exponent function, Weight function, Hardy-Hilbert's integral inequality, Hardy-Littlewood's integral inequality. |
|
| |
|
Date Received:
|
17/02/04 |
|
| |
|
Date Accepted:
|
10/11/05 |
|
| |
|
Subject Codes: |
26D15.
|
|
| |
|
Editors: |
Lubos Pick, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
In this paper, it is shown that an extended Hardy-Hilbert's integral inequality with weights can be established by introducing a power-exponent function of the form 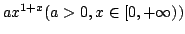 , and the coefficient , and the coefficient 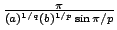 is shown to be the best possible constant in the inequality. In particular, for the case is shown to be the best possible constant in the inequality. In particular, for the case 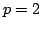 , some extensions on the classical Hilbert's integral inequality are obtained. As applications, generalizations of Hardy-Littlewood's integral inequality are given. , some extensions on the classical Hilbert's integral inequality are obtained. As applications, generalizations of Hardy-Littlewood's integral inequality are given.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|