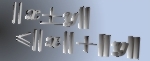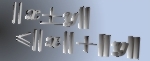JIPAM logo: Home Link
 
Home Editors Submissions Reviews Volumes RGMIA About Us
 

   
  Volume 7, Issue 1, Article 6
 
Some Inequalities Associated with a Linear Operator Defined for a Class of Analytic Functions
    Authors: S. R. Swamy,  
    Keywords: Analytic functions, Differential subordination, Ruscheweyh derivatives, Linear operator.  
    Date Received: 07/03/05  
    Date Accepted: 25/07/05  
    Subject Codes:

30C45.

  
    Editors: Herb Silverman,  
 
    Abstract:

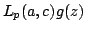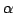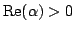In this paper, we give a sufficient condition on a linear operator $ L_p(a,c)g(z)$ which can guarantee that for $ alpha$ a complex number with $ func{Re}(alpha)>0$,

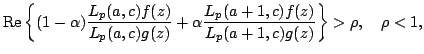$displaystyle func{Re}left{(1-alpha)frac{L_p(a,c)f(z)}{L_p(a,c)g(z)}+alpha frac{L_p(a+1,c)f(z)}{L_p(a+1,c)g(z)}right }>rho,quad rho </DIV> in the unit disk <IMG WIDTH=, implies
$displaystyle func{Re}left {frac{L_p(a,c)f(z)}{L_p(a,c)g(z)} right }>rho^{^{prime}}>rho, quad zin E. $
Some interesting applications of this result are also given.

         
       
  Download Screen PDF
  Download Print PDF
  Send this article to a friend
  Print this page
  

      search [advanced search] copyright 2003 terms and conditions login