| |
|
|
| |
Volume 6, Issue 4, Article 123 |
|
|
|
|
|
| |
On Global Approximation Properties of Abstract Integral Operators in Orlicz Spaces and Applications
|
| |
|
Authors: |
Carlo Bardaro, Ilaria Mantellini, |
|
| |
|
Keywords:
|
Modular approximation, nonlinear integral operators, regular families, singularity. |
|
| |
|
Date Received:
|
25/08/05 |
|
| |
|
Date Accepted:
|
01/09/05 |
|
| |
|
Subject Codes: |
41A25, 41A35, 47G10, 46E30.
|
|
| |
|
Editors: |
Sever S. Dragomir, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
In this paper we study approximation properties for the class of general integral operators of the form
where 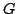 is a locally compact Hausdorff topological space, is a locally compact Hausdorff topological space, 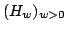 is a net of closed subsets of is a net of closed subsets of 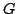 with suitable properties and, for every with suitable properties and, for every 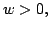 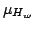 is a regular measure on is a regular measure on  We give pointwise, uniform and modular convergence theorems in abstract modular spaces and we apply the results to some kinds of discrete operators including the sampling type series. We give pointwise, uniform and modular convergence theorems in abstract modular spaces and we apply the results to some kinds of discrete operators including the sampling type series.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|



