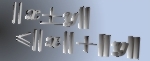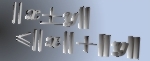| |
|
|
| |
Volume 6, Issue 4, Article 105 |
|
|
|
|
|
| |
On the Determinantal Inequalities
|
| |
|
Authors: |
Shilin Zhan, |
|
| |
|
Keywords:
|
Minkowski inequality, Determinantal inequality, Positive definite matrix, Eigenvalue. |
|
| |
|
Date Received:
|
24/08/05 |
|
| |
|
Date Accepted:
|
13/09/05 |
|
| |
|
Subject Codes: |
15A15, 15A57.
|
|
| |
|
Editors: |
Bicheng Yang, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
In this paper, we discuss the determinantal inequalities over arbitrary complex matrices, and give some sufficient conditions for
where 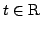 and and 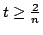 . If . If 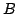 is nonsingular and is nonsingular and 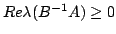 , the sufficient and necessary condition is given for the above equality at , the sufficient and necessary condition is given for the above equality at 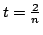 . The famous Minkowski inequality and many recent results about determinantal inequalities are extended. . The famous Minkowski inequality and many recent results about determinantal inequalities are extended.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|