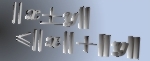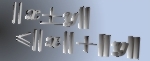| |
|
|
| |
Volume 6, Issue 1, Article 22 |
|
|
|
|
|
| |
A Class of Multivalent Functions with Positive Coefficients Defined by Convolution
|
| |
|
Authors: |
Rosihan M. Ali, M. Hussain Khan, V. Ravichandran, K.G. Subramanian, |
|
| |
|
Keywords:
|
Starlike function, Ruscheweyh derivative, Convolution, Positive coefficients, Coefficient inequalities, Growth and distortion theorems. |
|
| |
|
Date Received:
|
12/12/04 |
|
| |
|
Date Accepted:
|
27/01/05 |
|
| |
|
Subject Codes: |
30C45
|
|
| |
|
Editors: |
Herb Silverman, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
For a given 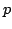 -valent analytic function -valent analytic function 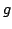 with positive coefficients in the open unit disk with positive coefficients in the open unit disk 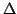 , we study a class of functions , we study a class of functions 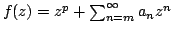 , , 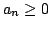 satisfying satisfying Coefficient inequalities, distortion and covering theorems, as well as closure theorems are determined. The results obtained extend several known results as special cases.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|