JIPAM

A Class of Multivalent Functions with Positive Coefficients Defined by Convolution  
 
  Authors: Rosihan M. Ali, M. Hussain Khan, V. Ravichandran, K.G. Subramanian,  
  Keywords: Starlike function, Ruscheweyh derivative, Convolution, Positive coefficients, Coefficient inequalities, Growth and distortion theorems.  
  Date Received: 12/12/04  
  Date Accepted: 27/01/05  
  Subject Codes:

30C45

  
  Editors: Herb Silverman,  
 
  Abstract:

For a given 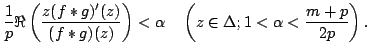$ p$-valent analytic function $ g$ with positive coefficients in the open unit disk $ Delta$, we study a class of functions $ f(z)=z^p+sum_{n=m}^infty a_nz^n$, $ a_ngeq 0$ satisfying

$displaystyle frac{1}{p}Releft( frac{z(f*g)^{prime}(z)}{(f*g)(z)}right) alpha quad left( zinDelta; 1alphafrac{m+p}{2p} right). $
Coefficient inequalities, distortion and covering theorems, as well as closure theorems are determined. The results obtained extend several known results as special cases.;


This article was printed from JIPAM
http://jipam.vu.edu.au

The URL for this article is:
http://jipam.vu.edu.au/article.php?sid=491