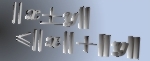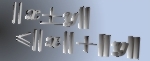| |
|
|
| |
Volume 6, Issue 1, Article 11 |
|
|
|
|
|
| |
On the Heisenberg-Weyl Inequality
|
| |
|
Authors: |
John Michael Rassias, |
|
| |
|
Keywords:
|
Heisenberg-Weyl Inequality, Uncertainty Principle, Absolute Moment, Gaussian, Extremum Principle. |
|
| |
|
Date Received:
|
20/09/04 |
|
| |
|
Date Accepted:
|
25/11/04 |
|
| |
|
Subject Codes: |
26Dxx, 30Xxx, 33Xxx, 42Xxx, 43Xxx, 60Xxx
|
|
| |
|
Editors: |
George Anastassiou, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
In 1927, W. Heisenberg demonstrated the impossibility of specifying simultaneously the position and the momentum of an electron within an atom.The well-known second moment Heisenberg-Weyl inequality states: Assume that 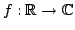 is a complex valued function of a random real variable is a complex valued function of a random real variable 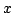 such that such that 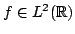 . Then the product of the second moment of the random real . Then the product of the second moment of the random real 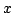 for for 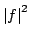 and the second moment of the random real and the second moment of the random real 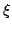 for for 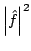 is at least is at least 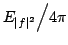 , where , where 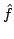 is the Fourier transform of is the Fourier transform of 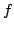 , such that , such that 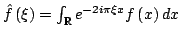 and and 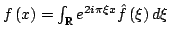 , , 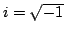 and and 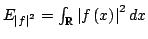 . In 2004, the author generalized the afore-mentioned result to the higher order absolute moments for . In 2004, the author generalized the afore-mentioned result to the higher order absolute moments for 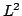 functions functions 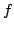 with orders of moments in the set of natural numbers . In this paper, a new generalization proof is established with orders of absolute moments in the set of non-negative real numbers. Afterwards, an application is provided by means of the well-known Euler gamma function and the Gaussian function and an open problem is proposed on some pertinent extremum principle. This inequality can be applied in harmonic analysis and quantum mechanics. with orders of moments in the set of natural numbers . In this paper, a new generalization proof is established with orders of absolute moments in the set of non-negative real numbers. Afterwards, an application is provided by means of the well-known Euler gamma function and the Gaussian function and an open problem is proposed on some pertinent extremum principle. This inequality can be applied in harmonic analysis and quantum mechanics.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|