| |
|
|
| |
Volume 6, Issue 1, Article 10 |
|
|
|
|
|
| |
Triple Solutions for a Higher-order Difference Equation
|
| |
|
Authors: |
Zengji Du, Chunyan Xue, Weigao Ge, |
|
| |
|
Keywords:
|
Discrete three-point boundary value problem; Multiple solutions; Green's function; Cone; Fixed point. |
|
| |
|
Date Received:
|
09/04/04 |
|
| |
|
Date Accepted:
|
24/12/04 |
|
| |
|
Subject Codes: |
39A10.
|
|
| |
|
Editors: |
Sever S. Dragomir, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
In this paper, we are concerned with the following  th difference equations th difference equations where 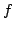 is continuous, is continuous, 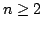 , , 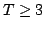 and and 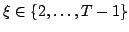 are three fixed positive integers, constant are three fixed positive integers, constant 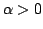 such that such that 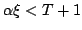 . Under some suitable conditions, we obtain the existence result of at least three positive solutions for the problem by using the Leggett-Williams fixed point theorem. . Under some suitable conditions, we obtain the existence result of at least three positive solutions for the problem by using the Leggett-Williams fixed point theorem.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|



