| |
|
|
| |
Volume 5, Issue 4, Article 102 |
|
|
|
|
|
| |
Estimators, Escort Probabilities, and $\phi$-Exponential Families in Statistical Physics
|
| |
|
Authors: |
Jan Naudts, |
|
| |
|
Keywords:
|
Escort probability, Lower bound of Cramer and Rao, Generalized exponential family, Statistical manifold, Nonextensive thermostatistics. |
|
| |
|
Date Received:
|
23/02/04 |
|
| |
|
Date Accepted:
|
11/11/04 |
|
| |
|
Subject Codes: |
82B30, 62H12
|
|
| |
|
Editors: |
Charles E. M. Pearce, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
The lower bound of Cramér and Rao is generalized to pairs of families of probability distributions, one of which is escort to the other. This bound is optimal for certain families, called 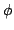 -exponential in the paper. Their dual structure is explored. They satisfy a variational principle with respect to an appropriately chosen entropy functional, which is the dual of a free energy functional.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|
Home
