| |
|
|
| |
Volume 5, Issue 4, Article 100 |
|
|
|
|
|
| |
On Hyers-Ulam Stability of Generalized Wilson's Equation
|
| |
|
Authors: |
Belaid Bouikhalene, |
|
| |
|
Keywords:
|
Functional equations, Hyers-Ulam stability, Wilson equation, Gelfand pairs. |
|
| |
|
Date Received:
|
20/05/04 |
|
| |
|
Date Accepted:
|
15/09/04 |
|
| |
|
Subject Codes: |
39B72.
|
|
| |
|
Editors: |
Laszlo Losonczi, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
In this paper, we study the Hyers-Ulam stability problem for the following functional equation  | (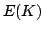 ) ) |
where  is a locally compact group, is a locally compact group, 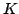 is a compact subgroup of is a compact subgroup of  , , 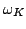 is the normalized Haar measure of is the normalized Haar measure of 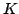 , , 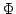 is a finite group of is a finite group of 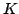 -invariant morphisms of -invariant morphisms of  and and 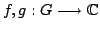 are continuous complex-valued functions such that are continuous complex-valued functions such that 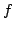 satisfies the Kannappan type condition, for all satisfies the Kannappan type condition, for all 
Our results generalize and extend the Hyers-Ulam stability obtained for the Wilson's functional equation.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|



