JIPAM logo: Home Link
 
Home Editors Submissions Reviews Volumes RGMIA About Us
 

   
  Volume 5, Issue 4, Article 87
 
Some Results on the Complex Oscillation Theory of Differential Equations with Polynomial Coefficients
    Authors: Benharrat Belaidi, Karima Hamani,  
    Keywords: Differential equations, Order of growth, Exponent of convergence of distinct zeros, Wiman-Valiron theory.  
    Date Received: 08/10/03  
    Date Accepted: 20/10/04  
    Subject Codes:

34M10, 34M05, 30D35.

  
    Editors: Hari M. Srivastava,  
 
    Abstract:

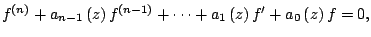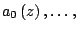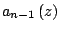In this paper, we study the possible orders of transcendental solutions of the differential equation $f^{left( nright) }+a_{n-1}left( zright) f^{left( n-1right) }+cdots +a_{1}left( zright) f^{prime }+a_{0}left( zright) f=0,$ where $a_{0}left( zright) ,dots ,$ $a_{n-1}left( zright) $ are nonconstant polynomials. 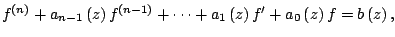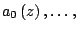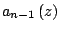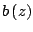We also investigate the possible orders and exponents of convergence of distinct zeros of solutions of non-homogeneous differential equation $f^{left( nright) }+a_{n-1}left( zright) f^{left( n-1right) }+cdots+a_{1}left( zright) f^{prime }+a_{0}left( zright) f=bleft( zright) ,$ where $a_{0}left( zright) ,dots ,$ $a_{n-1}left( zright) $ and $bleft( zright) $ are nonconstant polynomials. Several examples are given.

         
       
  Download Screen PDF
  Download Print PDF
  Send this article to a friend
  Print this page
  

      search [advanced search] copyright 2003 terms and conditions login