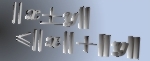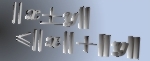JIPAM logo: Home Link
 
Home Editors Submissions Reviews Volumes RGMIA About Us
 

   
  Volume 5, Issue 3, Article 53
 
Kantorovich-Stancu Type Operators
    Authors: Dan Barbosu,  
    Keywords: Linear positive operators, Bernstein operator, Kantorovich operator, Stancu operator, First order modulus of smoothness, Shisha-Mond theorem.  
    Date Received: 10/11/03  
    Date Accepted: 29/04/04  
    Subject Codes:

41A36, 41A25

  
    Editors: A. M. Fink,  
 
    Abstract:

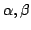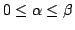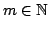Considering two given real parameters $ \alpha,\beta$ which satisfy the condition $ 0\leq\alpha\leq\beta$, D.D. Stancu ([11]) constructed and studied the linear positive operators $ P^{(\alpha,\beta)}_m:C([0,1])\to C([0,1])$, defined for any $ f\in C([0,1])$ and any $ m\in\mathbb{N}$ by

$\displaystyle \left(P^{(\alpha,\beta)}_m f\right)(x)=\sum^m_{k=0} p_{mk}(x)f\left(\frac{ k+\alpha}{m+\beta}\right).$    

In this paper, we are dealing with the Kantorovich form of the above operators. We construct the linear positive operators $ K^{(\alpha, \beta)}_m:L_1([0,1])\to C([0,1])$, defined for any $ f\in L_1([0,1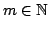])$ and any $ m\in\mathbb{N}$ by
$\displaystyle \left(K^{(\alpha,\beta)}_m f\right)(x)= (m+\beta+1)\sum^m_{k=0}p_{m,k}(x) \int^{\frac{k+\alpha+1}{m+\beta+1}}_{\frac{k+\alpha}{m+\beta+1}} f(s)ds$    

and we study some approximation properties of the sequence 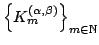$ \left\{K^{(\alpha,\beta)}_m\right\}_{m\in\mathbb{N}}$.

         
       
  Download Screen PDF
  Download Print PDF
  Send this article to a friend
  Print this page
  

      search [advanced search] copyright 2003 terms and conditions login