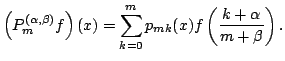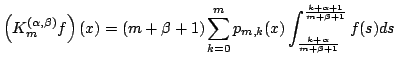JIPAM

Kantorovich-Stancu Type Operators  
 
  Authors: Dan Barbosu,  
  Keywords: Linear positive operators, Bernstein operator, Kantorovich operator, Stancu operator, First order modulus of smoothness, Shisha-Mond theorem.  
  Date Received: 10/11/03  
  Date Accepted: 29/04/04  
  Subject Codes:

41A36, 41A25

  
  Editors: A. M. Fink,  
 
  Abstract:

Considering two given real parameters $ \alpha,\beta$ which satisfy the condition $ 0\leq\alpha\leq\beta$, D.D. Stancu ([11]) constructed and studied the linear positive operators $ P^{(\alpha,\beta)}_m:C([0,1])\to C([0,1])$, defined for any $ f\in C([0,1])$ and any $ m\in\mathbb{N}$ by

$\displaystyle \left(P^{(\alpha,\beta)}_m f\right)(x)=\sum^m_{k=0} p_{mk}(x)f\left(\frac{ k+\alpha}{m+\beta}\right).$    

In this paper, we are dealing with the Kantorovich form of the above operators. We construct the linear positive operators $ K^{(\alpha, \beta)}_m:L_1([0,1])\to C([0,1])$, defined for any $ f\in L_1([0,1])$ and any $ m\in\mathbb{N}$ by
$\displaystyle \left(K^{(\alpha,\beta)}_m f\right)(x)= (m+\beta+1)\sum^m_{k=0}p_{m,k}(x) \int^{\frac{k+\alpha+1}{m+\beta+1}}_{\frac{k+\alpha}{m+\beta+1}} f(s)ds$    

and we study some approximation properties of the sequence $ \left\{K^{(\alpha,\beta)}_m\right\}_{m\in\mathbb{N}}$. ;


This article was printed from JIPAM
http://jipam.vu.edu.au

The URL for this article is:
http://jipam.vu.edu.au/article.php?sid=419