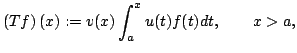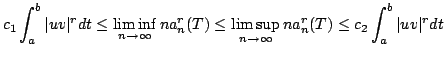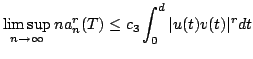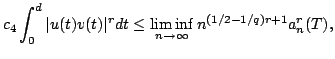JIPAM

Asymptotic Behavior Of The Approximation Numbers Of The Hardy-Type Operator From $L^p$ Into $L^q$  
 
  Authors: J. Lang, O. Mendez, A. Nekvinda,  
  Keywords: Approximation numbers, Hardy operator, Voltera operator.  
  Date Received: 17/12/03  
  Date Accepted: 04/02/04  
  Subject Codes:

Primary 46E30; Secondary 47B38

  
  Editors: Don B. Hinton,  
 
  Abstract:

We consider the Hardy-type operator

$displaystyle left(Tfright)(x) := v(x)int_a^x u(t)f(t) dt, qquad x>a,vspace{-3pt}$    

and establish properties of $ T$ as a map from $ L^p(a,b)$ into $ L^q(a,b)$ for $ 1ple q le 2$, $ 2le p le q infty$ and $ 1ple 2 le q infty$. The main result is that, with appropriate assumptions on $ u$ and $ v$, the approximation numbers $ a_n(T)$ of $ T$ satisfy the inequality

$displaystyle c_1 int_a^b vert uvvert^r dt le liminf_{n to infty} n a_n^... ...imsup_{nto infty} n a_n^r(T) le c_2 int_a^b vert uvvert^r dtvspace{-4pt}$    
when $ 1ple q le 2$ or $ 2le p le q infty$, and in the case $ 1ple 2 le q infty$ we have
$displaystyle limsup_{n to infty} n a_n^r(T) le c_{3} int_0^d vert u(t) v(t)vert^r dtvspace{-5pt}$    
and
$displaystyle c_{4} int_0^d vert u(t) v(t)vert^r dt le liminf_{n to infty} n^{(1/2-1/q)r+1} a^r_n(T),vspace{-5pt}$    
where $ r={frac{p^{prime}q }{p^{prime}+q}}$ and constants $ c_1,c_2,c_3,c_4$. Upper and lower estimates for the $ l^s$ and $ l^{s,k}$ norms of $ {a_n(T)}$ are also given.;


This article was printed from JIPAM
http://jipam.vu.edu.au

The URL for this article is:
http://jipam.vu.edu.au/article.php?sid=370