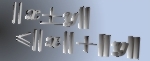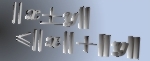| |
|
|
| |
Volume 5, Issue 1, Article 17 |
|
|
|
|
|
| |
Some Geometric Inequalities For The Holmes-Thompson Definitions Of Volume And Surface Area In Minkowski Spaces
|
| |
|
Authors: |
Zokhrab Mustafaev, |
|
| |
|
Keywords:
|
Convex body, Isoperimetrix, Mixed volume, Projection body, the Holmes-Thompson definitions of volume and surface area. |
|
| |
|
Date Received:
|
16/06/03 |
|
| |
|
Date Accepted:
|
13/01/04 |
|
| |
|
Subject Codes: |
52A20, 46B20.
|
|
| |
|
Editors: |
Constantin P. Niculescu, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
Let 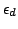 be the volume of the be the volume of the 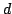 -dimensional standard Euclidean unit ball. In standard Euclidean space the ratio of the surface area of the unit ball to the volume is equal to the dimension of the space. In Minkowski space (finite dimensional Banach space) where the volume has been normalized according to the Holmes-Thompson definition the ratio is known to lie between -dimensional standard Euclidean unit ball. In standard Euclidean space the ratio of the surface area of the unit ball to the volume is equal to the dimension of the space. In Minkowski space (finite dimensional Banach space) where the volume has been normalized according to the Holmes-Thompson definition the ratio is known to lie between 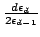 and and 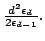 We show that when We show that when 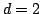 the lower bound is 2 and equality is achieved if and only if Minkowski space is affinely equivalent to Euclidean, i.e., the unit ball is an ellipse. the lower bound is 2 and equality is achieved if and only if Minkowski space is affinely equivalent to Euclidean, i.e., the unit ball is an ellipse.
Stronger criteria involving the inner and outer radii is also obtained for the 2-dimension spaces. In the higher dimensions we discuss the relationship of the Petty's conjecture to the case for equality in the lower limit.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|