JIPAM
| The Boundary of Weighted Analytic Centers for Linear Matrix Inequalities | |||||||
| Authors: | Shafiu Jibrin, James W. Swift, | ||||||
| Keywords: | Linear matrix inequalities, Analytic center, Central path, Semidefinite programming. | ||||||
| Date Received: | 28/10/03 | ||||||
| Date Accepted: | 03/02/04 | ||||||
| Subject Codes: |
90C22, 15A39, 49M15, 90C53 |
||||||
| Editors: | Fuzhen Zhang, | ||||||
| Abstract: |
We study the boundary of the region of weighted analytic centers for linear matrix inequality constraints. Let
over We introduce the concept of the frame of | ||||||
http://jipam.vu.edu.au
The URL for this article is:
http://jipam.vu.edu.au/article.php?sid=366
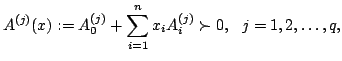
![$displaystyle {phi _{omega }(x):=sum_{j=1}^{q}omega _{j}log det [A^{(j)}(x)]^{-1}}$](images/158_03_JIPAM/img13.gif)