| |
|
|
| |
Volume 3, Issue 5, Article 84 |
|
|
|
|
|
| |
Asymptotic Expansion of the Equipoise Curve of a Polynomial Inequality
|
| |
|
Authors: |
Roger B. Eggleton, William P. Galvin, |
|
| |
|
Keywords:
|
Polynomial inequality, Catalan numbers. |
|
| |
|
Date Received:
|
28/08/02 |
|
| |
|
Date Accepted:
|
08/11/02 |
|
| |
|
Subject Codes: |
26D05,26C99,05A99
|
|
| |
|
Editors: |
Hillel Gauchman, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
For any  define define 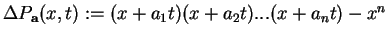 and and 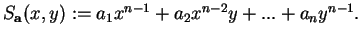 The two homogeneous polynomials The two homogeneous polynomials 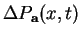 and and 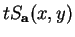 are comparable in the positive octant are comparable in the positive octant 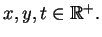 Recently the authors [2] studied the inequality Recently the authors [2] studied the inequality 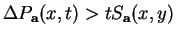 and its reverse and noted that the boundary between the corresponding regions in the positive octant is fully determined by the equipoise curve and its reverse and noted that the boundary between the corresponding regions in the positive octant is fully determined by the equipoise curve  In the present paper the asymptotic expansion of the equipoise curve is shown to exist, and is determined both recursively and explicitly. Several special cases are then examined in detail, including the general solution when In the present paper the asymptotic expansion of the equipoise curve is shown to exist, and is determined both recursively and explicitly. Several special cases are then examined in detail, including the general solution when 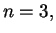 where the coefficients involve a type of generalised Catalan number, and the case where where the coefficients involve a type of generalised Catalan number, and the case where 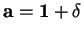 is a sequence in which each term is close to 1. A selection of inequalities implied by these results completes the paper. is a sequence in which each term is close to 1. A selection of inequalities implied by these results completes the paper.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|



