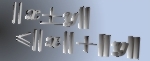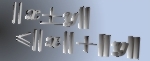| |
|
|
| |
Volume 3, Issue 5, Article 80 |
|
|
|
|
|
| |
Reverse Convolution Inequalities and Applications to Inverse Heat Source Problems
|
| |
|
Authors: |
Saburou Saitoh, Vu Kim Tuan, Masahiro Yamamoto, |
|
| |
|
Keywords:
|
Convolution, Heat source, Weighted convolution inequalities, Young's inequality, Hölder's inequality, Reverse Hölder's inequality, Green's function, Stability in inverse problems, Volterra's equation, Conditional stability of Hölder type, Analytic semigroup, Interpolation inequality, Sobolev inequality. |
|
| |
|
Date Received:
|
02/04/02 |
|
| |
|
Date Accepted:
|
30/10/02 |
|
| |
|
Subject Codes: |
44A35,26D20
|
|
| |
|
Editors: |
Sever S. Dragomir, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
We introduce reverse convolution inequalities obtained recently and at the same time, we give new type reverse convolution inequalities and their important applications to inverse source problems. We consider the inverse problem of determining 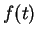 , , 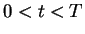 , in the heat source of the heat equation , in the heat source of the heat equation 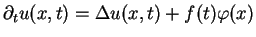 , , 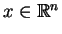 , , 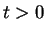 from the observation from the observation 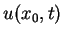 , , 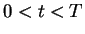 , at a remote point , at a remote point 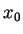 away from the support of away from the support of 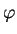 . Under an a priori assumption that . Under an a priori assumption that 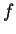 changes the signs at most changes the signs at most 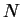 -times, we give a conditional stability of Hölder type, as an example of applications. -times, we give a conditional stability of Hölder type, as an example of applications.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|