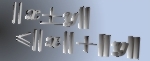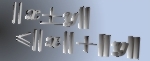| |
|
|
| |
Volume 10, Issue 3, Article 74 |
|
|
|
|
|
| |
On the Interpoint Distance Sum Inequality
|
| |
|
Authors: |
Yong Xia, Hong-Ying Liu, |
|
| |
|
Keywords:
|
Combinatorial geometry, Distance geometry, Interpoint distance sum inequality, Optimization. |
|
| |
|
Date Received:
|
10/04/2009 |
|
| |
|
Date Accepted:
|
28/09/2009 |
|
| |
|
Subject Codes: |
51D20, 51K05, 52C26.
|
|
| |
|
Editors: |
Peter S. Bullen, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
Let 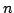 points be arbitrarily placed in points be arbitrarily placed in 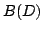 , a disk in , a disk in 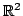 having diameter having diameter 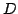 . Denote by . Denote by 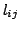 the Euclidean distance between point the Euclidean distance between point 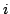 and and 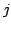 . In this paper, we show . In this paper, we show We then extend the result to 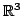 . .
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|