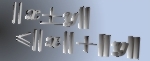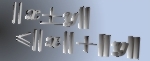| |
|
|
| |
Volume 10, Issue 3, Article 71 |
|
|
|
|
|
| |
Coefficient Bounds for Meromorphic Starlike and Convex Functions
|
| |
|
Authors: |
See Keong Lee, V. Ravichandran, Supramaniam Shamani, |
|
| |
|
Keywords:
|
Univalent meromorphic functions; starlike function, convex function, Fekete-Szegö inequality. |
|
| |
|
Date Received:
|
30/01/2008 |
|
| |
|
Date Accepted:
|
03/05/2009 |
|
| |
|
Subject Codes: |
Primary 30C45, Secondary 30C80.
|
|
| |
|
Editors: |
Sever S. Dragomir, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
In this paper, some subclasses of meromorphic univalent functions in the unit disk 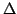 are extended. Let are extended. Let  denote the class of normalized univalent meromorphic functions denote the class of normalized univalent meromorphic functions 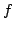 in in 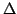 with a simple pole at with a simple pole at 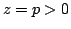 . Let . Let  be a function with positive real part on be a function with positive real part on 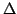 with with 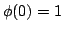 , , 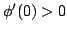 which maps which maps  onto a region starlike with respect to onto a region starlike with respect to  which is symmetric with respect to the real axis. The class which is symmetric with respect to the real axis. The class 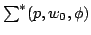 consists of functions consists of functions 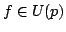 satisfying satisfying The class 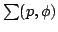 consists of functions consists of functions 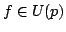 satisfying The bounds for satisfying The bounds for 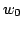 and some initial coefficients of and some initial coefficients of 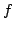 in in 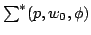 and and 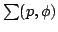 are obtained. are obtained.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|