| |
|
|
| |
Volume 10, Issue 3, Article 64 |
|
|
|
|
|
| |
Sum of Squares of Degrees in a Graph
|
| |
|
Authors: |
Bernardo M. Ábrego, Silvia Fernández-Merchant, Michael G. Neubauer, William Watkins, |
|
| |
|
Keywords:
|
Graph, Degree sequence, Threshold graph, Pell's Equation, Partition, Density. |
|
| |
|
Date Received:
|
18/09/2008 |
|
| |
|
Date Accepted:
|
19/06/2009 |
|
| |
|
Subject Codes: |
05C07, 05C35.
|
|
| |
|
Editors: |
Chi-Kwong Li, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
Let 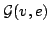 be the set of all simple graphs with be the set of all simple graphs with 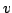 vertices and vertices and 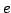 edges and let edges and let 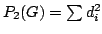 denote the sum of the squares of the degrees, denote the sum of the squares of the degrees, 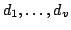 , of the vertices of , of the vertices of 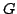 . . It is known that the maximum value of 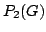 for for 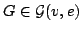 occurs at one or both of two special graphs in occurs at one or both of two special graphs in 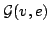 --the quasi-star graph or the quasi-complete graph. For each pair --the quasi-star graph or the quasi-complete graph. For each pair 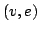 , we determine which of these two graphs has the larger value of , we determine which of these two graphs has the larger value of 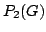 . We also determine all pairs . We also determine all pairs 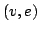 for which the values of for which the values of 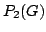 are the same for the quasi-star and the quasi-complete graph. In addition to the quasi-star and quasi-complete graphs, we find all other graphs in are the same for the quasi-star and the quasi-complete graph. In addition to the quasi-star and quasi-complete graphs, we find all other graphs in 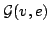 for which the maximum value of for which the maximum value of 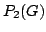 is attained. Density questions posed by previous authors are examined. is attained. Density questions posed by previous authors are examined.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|



