| |
|
|
| |
Volume 10, Issue 3, Article 63 |
|
|
|
|
|
| |
An Upper Bound for the Determinant of a Matrix with given Entry Sum and Square Sum
|
| |
|
Authors: |
Ortwin Gasper, Hugo Pfoertner, Markus Sigg, |
|
| |
|
Keywords:
|
Determinant, Matrix Inequality, Hadamard's Determinant Theorem, Hadamard Matrix. |
|
| |
|
Date Received:
|
05/03/2009 |
|
| |
|
Date Accepted:
|
15/09/2009 |
|
| |
|
Subject Codes: |
15A15, 15A45, 26D07.
|
|
| |
|
Editors: |
Sever S. Dragomir, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
By deducing characterisations of the matrices which have maximal determinant in the set of matrices with given entry sum and square sum, we prove the inequality  for real for real 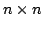 -matrices -matrices 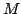 , where , where 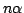 and and 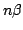 are the sum of the entries and the sum of the squared entries of are the sum of the entries and the sum of the squared entries of 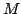 , respectively, and , respectively, and 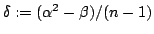 , provided that , provided that 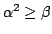 . This result is applied to find an upper bound for the determinant of a matrix whose entries are a permutation of an arithmetic progression. . This result is applied to find an upper bound for the determinant of a matrix whose entries are a permutation of an arithmetic progression.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|



