| |
|
|
| |
Volume 9, Issue 4, Article 104 |
|
|
|
|
|
| |
A Multinomial Extension of an Inequality of Haber
|
| |
|
Authors: |
Hacčne Belbachir, |
|
| |
|
Keywords:
|
Haber inequality, multinomial coefficient, symmetric functions. |
|
| |
|
Date Received:
|
10/07/08 |
|
| |
|
Date Accepted:
|
17/09/08 |
|
| |
|
Subject Codes: |
05A20, 05E05.
|
|
| |
|
Editors: |
László Tóth, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
In this paper, we establish the following: Let 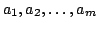 be non negative real numbers, then for all be non negative real numbers, then for all 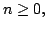 we have we have The case 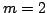 gives the Haber inequality. We apply the result to find lower bounds for the sum of reciprocals of multinomial coefficients and for symmetric functions. gives the Haber inequality. We apply the result to find lower bounds for the sum of reciprocals of multinomial coefficients and for symmetric functions.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|