| |
|
|
| |
Volume 9, Issue 4, Article 94 |
|
|
|
|
|
| |
A Non Local Quantitative Characterization of ellipses Leading to a Solvable Differential Relation
|
| |
|
Authors: |
M. Amar, L.R. Berrone, R. Gianni, |
|
| |
|
Keywords:
|
Convex sets, asymptotic expansion, ordinary differential equations. |
|
| |
|
Date Received:
|
14/02/08 |
|
| |
|
Date Accepted:
|
03/07/08 |
|
| |
|
Subject Codes: |
52A10, 41A58, 34A05.
|
|
| |
|
Editors: |
Catherine Bandle, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
In this paper we prove that there are no domains 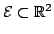 , other than the ellipses, such that the Lebesgue measure of the intersection of , other than the ellipses, such that the Lebesgue measure of the intersection of  and its homothetic image and its homothetic image 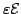 translated to a boundary point translated to a boundary point 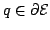 is independent of is independent of 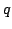 , provided that , provided that  is "centered" at a certain interior point is "centered" at a certain interior point 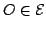 (the center of homothety). (the center of homothety).
Similar problems arise in various fields of mathematics, including, for example, the study of stationary isothermal surfaces and rearrangements.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|



